| Citation: | Buono WT, Forbes A. Nonlinear optics with structured light. Opto-Electron Adv 5, 210174 (2022). doi: 10.29026/oea.2022.210174 |
-
Abstract
The interest in tailoring light in all its degrees of freedom is steadily gaining traction, driven by the tremendous developments in the toolkit for the creation, control and detection of what is now called structured light. Because the complexity of these optical fields is generally understood in terms of interference, the tools have historically been linear optical elements that create the desired superpositions. For this reason, despite the long and impressive history of nonlinear optics, only recently has the spatial structure of light in nonlinear processes come to the fore. In this review we provide a concise theoretical framework for understanding nonlinear optics in the context of structured light, offering an overview and perspective on the progress made, and the challenges that remain. -
-
References
[1] Forbes A, de Oliveira M, Dennis MR. Structured light. Nat Photonics 15, 253–262 (2021). doi: 10.1038/s41566-021-00780-4 [2] Otte E, Alpmann C, Denz C. Polarization singularity explosions in tailored light fields. Laser Photonics Rev 12, 1700200 (2018). doi: 10.1002/lpor.201700200 [3] Rosales-Guzmán C, Ndagano B, Forbes A. A review of complex vector light fields and their applications. J Opt 20, 123001 (2018). doi: 10.1088/2040-8986/aaeb7d [4] Willner AE, Huang H, Yan Y, Ren Y, Ahmed N et al. Optical communications using orbital angular momentum beams. Adv Opt Photonics 7, 66–106 (2015). doi: 10.1364/AOP.7.000066 [5] Padgett MJ. Orbital angular momentum 25 years on [Invited]. Opt Express 25, 11265–11274 (2017). doi: 10.1364/OE.25.011265 [6] Forbes A, Nape I. Quantum mechanics with patterns of light: progress in high dimensional and multidimensional entanglement with structured light. AVS Quantum Sci 1, 011701 (2019). doi: 10.1116/1.5112027 [7] Erhard M, Fickler R, Krenn M, Zeilinger A. Twisted photons: new quantum perspectives in high dimensions. Light Sci Appl 7, 17146 (2018). doi: 10.1038/lsa.2017.146 [8] Larocque H, Sugic D, Mortimer D, Taylor AJ, Fickler R et al. Reconstructing the topology of optical polarization knots. Nat Phys 14, 1079–1082 (2018). doi: 10.1038/s41567-018-0229-2 [9] Galvez EJ, Rojec BL, Kumar V, Viswanathan NK. Generation of isolated asymmetric umbilics in light’s polarization. Phys Rev A 89, 031801 (2014). doi: 10.1103/PhysRevA.89.031801 [10] Zdagkas A, Shen YJ, McDonnell C, Deng J, Li G et al. Observation of toroidal pulses of light. arXiv: 2102.03636 (2021). [11] Keren-Zur S, Tal M, Fleischer S, Mittleman DM, Ellenbogen T. Generation of spatiotemporally tailored terahertz wavepackets by nonlinear metasurfaces. Nat Commun 10, 1778 (2019). doi: 10.1038/s41467-019-09811-9 [12] Bauer T, Banzer P, Karimi E, Orlov S, Rubano A et al. Optics. Observation of optical polarization Möbius strips. Science 347, 964–966 (2015). doi: 10.1126/science.1260635 [13] Dallaire M, McCarthy N, Piché M. Spatiotemporal Bessel beams: theory and experiments. Opt Express 17, 18148–18164 (2009). doi: 10.1364/OE.17.018148 [14] Chong A, Wan CH, Chen J, Zhan QW. Generation of spatiotemporal optical vortices with controllable transverse orbital angular momentum. Nat Photonics 14, 350–354 (2020). doi: 10.1038/s41566-020-0587-z [15] Kondakci HE, Abouraddy AF. Diffraction-free space-time light sheets. Nat Photonics 11, 733–740 (2017). doi: 10.1038/s41566-017-0028-9 [16] Shen YJ, Hou YN, Papasimakis N, Zheludev NI. Supertoroidal light pulses as electromagnetic skyrmions propagating in free space. Nat Commun 12, 5891 (2021). doi: 10.1038/s41467-021-26037-w [17] Shen YJ, Nape I, Yang XL, Fu X, Gong ML et al. Creation and control of high-dimensional multi-partite classically entangled light. Light Sci Appl 10, 50 (2021). doi: 10.1038/s41377-021-00493-x [18] Shen YJ, Yang XL, Naidoo D, Fu X, Forbes A. Structured ray-wave vector vortex beams in multiple degrees of freedom from a laser. Optica 7, 820–831 (2020). doi: 10.1364/OPTICA.382994 [19] Spreeuw RJC. A classical analogy of entanglement. Found Phys 28, 361–374 (1998). doi: 10.1023/A:1018703709245 [20] Ndagano B, Perez-Garcia B, Roux FS, McLaren M, Rosales-Guzman C et al. Characterizing quantum channels with non-separable states of classical light. Nat Phys 13, 397–402 (2017). doi: 10.1038/nphys4003 [21] Forbes A, Aiello A, Ndagano B. Classically entangled light. Prog Opt 64, 99–153 (2019). [22] Aiello A, Banzer P, Neugebauer M, Leuchs G. From transverse angular momentum to photonic wheels. Nat Photonics 9, 789–795 (2015). doi: 10.1038/nphoton.2015.203 [23] Padgett MJ, Courtial J. Poincaré-sphere equivalent for light beams containing orbital angular momentum. Opt Lett 24, 430–432 (1999). doi: 10.1364/OL.24.000430 [24] Milione G, Sztul HI, Nolan DA, Alfano RR. Higher-order poincaré sphere, stokes parameters, and the angular momentum of light. Phys Rev Lett 107, 053601 (2011). doi: 10.1103/PhysRevLett.107.053601 [25] Shen YJ. Rays, waves, SU(2) symmetry and geometry: toolkits for structured light. J Opt 23, 124004 (2021). doi: 10.1088/2040-8986/ac3676 [26] Mazilu M, Stevenson DJ, Gunn-Moore F, Dholakia K. Light beats the spread: “non-diffracting” beams. Laser Photonics Rev 4, 529–547 (2010). doi: 10.1002/lpor.200910019 [27] Gossman D, Perez-Garcia B, Hernandez-Aranda RI, Forbes A. Optical interference with digital holograms. Am J Phys 84, 508–516 (2016). doi: 10.1119/1.4948604 [28] Ayuso D, Neufeld O, Ordonez AF, Decleva P, Lerner G et al. Synthetic chiral light for efficient control of chiral light-matter interaction. Nat Photonics 13, 866–871 (2019). doi: 10.1038/s41566-019-0531-2 [29] Maiman TH. Stimulated optical radiation in ruby. Nature 187, 493–494 (1960). doi: 10.1038/187493a0 [30] Franken PA, Hill AE, Peters CW, Weinreich G. Generation of optical harmonics. Phys Rev Lett 7, 118–119 (1961). doi: 10.1103/PhysRevLett.7.118 [31] New GHC, Ward JF. Optical third-harmonic generation in gases. Phys Rev Lett 19, 556–559 (1967). doi: 10.1103/PhysRevLett.19.556 [32] Simon HJ, Bloembergen N. Second-harmonic light generation in crystals with natural optical activity. Phys Rev 171, 1104–1114 (1968). doi: 10.1103/PhysRev.171.1104 [33] Abraham NB, Firth WJ. Overview of transverse effects in nonlinear-optical systems. J Opt Soc Am B 7, 951–962 (1990). [34] Basistiy IV, Bazhenov VY, Soskin MS, Vasnetsov MV. Optics of light beams with screw dislocations. Opt Commun 103, 422–428 (1993). doi: 10.1016/0030-4018(93)90168-5 [35] Shen YJ, Wang XJ, Xie ZW, Min CJ, Fu X et al. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities. Light Sci Appl 8, 90 (2019). doi: 10.1038/s41377-019-0194-2 [36] Dholakia K, Simpson NB, Padgett MJ, Allen L. Second-harmonic generation and the orbital angular momentum of light. Phys Rev A 54, R3742–R3745 (1996). doi: 10.1103/PhysRevA.54.R3742 [37] Mair A, Vaziri A, Weihs G, Zeilinger A. Entanglement of the orbital angular momentum states of photons. Nature 412, 313–316 (2001). doi: 10.1038/35085529 [38] Boyd RW. Nonlinear Optics 3rd ed (Elsevier, Oxford, 2008). [39] Murti YVGS, Vijayan C. Essentials of Nonlinear Optics (John Wiley & Sons, New York, 2014). [40] Shen YR. The Principles of Nonlinear Optics (John Wiley & Sons, New York, 1984). [41] Singh K, Buono WT, Chavez-Cerda S, Forbes A. Demonstrating arago-fresnel laws with Bessel beams from vectorial axicons. J Opt Soc Am A 38, 1248–1254 (2021). doi: 10.1364/JOSAA.431186 [42] Zhou ZY, Li Y, Ding DS, Jiang YK, Zhang W et al. Generation of light with controllable spatial patterns via the sum frequency in quasi-phase matching crystals. Sci Rep 4, 5650 (2014). [43] Shao GH, Wu ZJ, Chen JH, Xu F, Lu YQ. Nonlinear frequency conversion of fields with orbital angular momentum using quasi-phase-matching. Phys Rev A 88, 063827 (2013). doi: 10.1103/PhysRevA.88.063827 [44] Steinlechner F, Hermosa N, Pruneri V, Torres JP. Frequency conversion of structured light. Sci Rep 6, 21390 (2016). doi: 10.1038/srep21390 [45] Li Y, Zhou ZY, Ding DS, Shi BS. Sum frequency generation with two orbital angular momentum carrying laser beams. J Opt Soc Am B 32, 407–411 (2015). doi: 10.1364/JOSAB.32.000407 [46] Schwob C, Cohadon PF, Fabre C, Marte MAM, Ritsch H et al. Transverse effects and mode couplings in OPOS. Appl Phys B 66, 685–699 (1998). doi: 10.1007/s003400050455 [47] Buono WT, Moraes LFC, Huguenin JAO, Souza CER, Khoury AZ. Arbitrary orbital angular momentum addition in second harmonic generation. New J Phys 16, 093041 (2014). doi: 10.1088/1367-2630/16/9/093041 [48] Roger T, Heitz JJF, Wright EM, Faccio D. Non-collinear interaction of photons with orbital angular momentum. Sci Rep 3, 3491 (2013). doi: 10.1038/srep03491 [49] Bovino FA, Braccini M, Giardina M, Sibilia C. Orbital angular momentum in noncollinear second-harmonic generation by off-axis vortex beams. J Opt Soc Am B 28, 2806–2811 (2011). doi: 10.1364/JOSAB.28.002806 [50] Buono WT, Santiago J, Pereira LJ, Tasca DS, Dechoum K et al. Polarization-controlled orbital angular momentum switching in nonlinear wave mixing. Opt Lett 43, 1439–1442 (2018). doi: 10.1364/OL.43.001439 [51] Courtial J, Dholakia K, Allen L, Padgett MJ. Second-harmonic generation and the conservation of orbital angular momentum with high-order Laguerre-Gaussian modes. Phys Rev A 56, 4193–4196 (1997). doi: 10.1103/PhysRevA.56.4193 [52] Pereira LJ, Buono WT, Tasca DS, Dechoum K, Khoury AZ. Orbital-angular-momentum mixing in type-II second-harmonic generation. Phys Rev A 96, 053856 (2017). doi: 10.1103/PhysRevA.96.053856 [53] Pires DG, Rocha JCA, Jesus-Silva AJ, Fonseca EJS. Higher radial orders of Laguerre-Gaussian beams in nonlinear wave mixing processes. J Opt Soc Am B 37, 1328–1332 (2020). doi: 10.1364/JOSAB.384112 [54] Wu HJ, Mao LW, Yang YJ, Rosales-Guzmán C, Gao W et al. Radial modal transitions of Laguerre-Gauss modes during parametric up-conversion: towards the full-field selection rule of spatial modes. Phys Rev A 101, 063805 (2020). doi: 10.1103/PhysRevA.101.063805 [55] Buono WT, Santos A, Maia MR, Pereira LJ, Tasca DS et al. Chiral relations and radial-angular coupling in nonlinear interactions of optical vortices. Phys Rev A 101, 043821 (2020). doi: 10.1103/PhysRevA.101.043821 [56] Alves GB, Barros RF, Tasca DS, Souza CER, Khoury AZ. Conditions for optical parametric oscillation with a structured light pump. Phys Rev A 98, 063825 (2018). doi: 10.1103/PhysRevA.98.063825 [57] Pires DG, Rocha JCA, da Silva MVEC, Jesus-Silva AJ, Fonseca EJS. Mixing Ince-Gaussian modes through sum-frequency generation. J Opt Soc Am B 37, 2815–2821 (2020). doi: 10.1364/JOSAB.401001 [58] Yang HR, Wu HJ, Gao W, Rosales-Guzmán C, Zhu ZH. Parametric upconversion of Ince-Gaussian modes. Opt Lett 45, 3034–3037 (2020). doi: 10.1364/OL.393146 [59] Jarutis V, Matijošius A, Smilgevičius V, Stabinis A. Second harmonic generation of higher-order Bessel beams. Opt Commun 185, 159–169 (2000). doi: 10.1016/S0030-4018(00)00974-3 [60] Ding DS, Lu JY. Second-harmonic generation of the nth-order Bessel beam. Phys Rev E 61, 2038–2041 (2000). doi: 10.1103/PhysRevE.61.2038 [61] Shinozaki K, Xu CQ, Sasaki H, Kamijoh T. A comparison of optical second-harmonic generation efficiency using Bessel and Gaussian beams in bulk crystals. Opt Commun 133, 300–304 (1997). doi: 10.1016/S0030-4018(96)00413-0 [62] Rao AS, Yadav D, Samanta GK. Nonlinear frequency conversion of 3D optical bottle beams generated using a single axicon. Opt Lett 46, 657–660 (2021). doi: 10.1364/OL.413899 [63] Pires DG, Rocha JCA, Jesus-Silva AJ, Fonseca EJS. Interaction of fractional orbital angular momentum in two-wave mixing processes. J Opt 22, 035502 (2020). doi: 10.1088/2040-8986/ab6ae6 [64] Dai KJ, Miller JK, Li WZ, Watkins RJ, Johnson EG. Fractional orbital angular momentum conversion in second-harmonic generation with an asymmetric perfect vortex beam. Opt Lett 46, 3332–3335 (2021). doi: 10.1364/OL.428859 [65] Rao AS. Characterization of off-axis phase singular optical vortex and its nonlinear wave-mixing to generate control broad OAM spectra. Phys Scr 95, 055508 (2020). doi: 10.1088/1402-4896/ab7b09 [66] Zhdanova AA, Shutova M, Bahari A, Zhi MC, Sokolov AV. Topological charge algebra of optical vortices in nonlinear interactions. Opt Express 23, 34109–34117 (2015). doi: 10.1364/OE.23.034109 [67] Wadhwa J, Singh A. Second harmonic generation of self-focused Hermite-Gaussian laser beam in collisional plasma. Optik 202, 162326 (2020). doi: 10.1016/j.ijleo.2019.01.116 [68] Xiong XYZ, Al-Jarro A, Jiang LJ, Panoiu NC, Sha WEI. Mixing of spin and orbital angular momenta via second-harmonic generation in plasmonic and dielectric chiral nanostructures. Phys Rev B 95, 165432 (2017). doi: 10.1103/PhysRevB.95.165432 [69] Wu HJ, Zhao B, Rosales-Guzmán C, Gao W, Shi BS et al. Spatial-polarization-independent parametric up-conversion of vectorially structured light. Phys Rev Appl 13, 064041 (2020). doi: 10.1103/PhysRevApplied.13.064041 [70] da Silva BP, Buono WT, Pereira LJ, Tasca DS, Dechoum K et al. Spin to orbital angular momentum transfer in frequency up-conversion. Nanophotonics 11, 771–778 (2021). doi: 10.1515/nanoph-2021-0493 [71] Sephton B, Vallés A, Steinlechner F, Konrad T, Torres JP et al. Spatial mode detection by frequency upconversion. Opt Lett 44, 586–589 (2019). doi: 10.1364/OL.44.000586 [72] Pires DG, Rocha JCA, Jesus-Silva AJ, Fonseca EJS. Suitable state bases for nonlinear optical mode conversion protocols. Opt Lett 45, 4064–4067 (2020). doi: 10.1364/OL.394640 [73] Fang XY, Kuang ZY, Chen P, Yang HC, Li Q et al. Examining second-harmonic generation of high-order Laguerre-Gaussian modes through a single cylindrical lens. Opt Lett 42, 4387–4390 (2017). doi: 10.1364/OL.42.004387 [74] Kumar S, Zhang H, Maruca S, Huang YP. Mode-selective image upconversion. Opt Lett 44, 98–101 (2019). doi: 10.1364/OL.44.000098 [75] Zhang H, Kumar S, Huang YP. Mode selective up-conversion detection with turbulence. Sci Rep 9, 17481 (2019). doi: 10.1038/s41598-019-53914-8 [76] Pinnell J, Nape I, Sephton B, Cox MA, Rodríguez-Fajardo V et al. Modal analysis of structured light with spatial light modulators: a practical tutorial. J Opt Soc Am A 37, C146–C160 (2020). doi: 10.1364/JOSAA.398712 [77] Qiu XD, Li FS, Zhang WH, Zhu ZH, Chen LX. Spiral phase contrast imaging in nonlinear optics: seeing phase objects using invisible illumination. Optica 5, 208–212 (2018). doi: 10.1364/OPTICA.5.000208 [78] Xu DF, Ma TL, Qiu XD, Zhang WH, Chen LX. Implementing selective edge enhancement in nonlinear optics. Opt Express 28, 32377–32385 (2020). doi: 10.1364/OE.404594 [79] Hong L, Lin F, Qiu XD, Chen LX. Second harmonic generation based joint transform correlator for human face and QR code recognitions. Appl Phys Lett 116, 231101 (2020). doi: 10.1063/5.0001301 [80] Zhang L, Qiu XD, Li FS, Liu HG, Chen XF et al. Second harmonic generation with full Poincaré beams. Opt Express 26, 11678–1184 (2018). doi: 10.1364/OE.26.011678 [81] Liu HG, Li H, Zheng YL, Chen XF. Nonlinear frequency conversion and manipulation of vector beams. Opt Lett 43, 5981–5984 (2018). doi: 10.1364/OL.43.005981 [82] Saripalli RK, Ghosh A, Chaitanya NA, Samanta GK. Frequency-conversion of vector vortex beams with space-variant polarization in single-pass geometry. Appl Phys Lett 115, 051101 (2019). doi: 10.1063/1.5111593 [83] Wu HJ, Zhou ZY, Gao W, Shi BS, Zhu ZH. Dynamic tomography of the spin-orbit coupling in nonlinear optics. Phys Rev A 99, 023830 (2019). doi: 10.1103/PhysRevA.99.023830 [84] Bouchard F, Larocque H, Yao AM, Travis C, De Leon I et al. Polarization shaping for control of nonlinear propagation. Phys Rev Lett 117, 233903 (2016). doi: 10.1103/PhysRevLett.117.233903 [85] Yang C, Zhou ZY, Li Y, Li YH, Liu SL et al. Nonlinear frequency conversion and manipulation of vector beams in a Sagnac loop. Opt Lett 44, 219–222 (2019). doi: 10.1364/OL.44.000219 [86] Ren ZC, Lou YC, Cheng ZM, Fan L, Ding JP et al. Optical frequency conversion of light with maintaining polarization and orbital angular momentum. Opt Lett 46, 2300–2303 (2021). doi: 10.1364/OL.419753 [87] Samim M, Krouglov S, Barzda V. Nonlinear Stokes-Mueller polarimetry. Phys Rev A 93, 013847 (2016). doi: 10.1103/PhysRevA.93.013847 [88] Ribeiro PHS, Caetano DP, Almeida MP, Huguenin JA, dos Santos BC et al. Observation of image transfer and phase conjugation in stimulated down-conversion. Phys Rev Lett 87, 133602 (2001). doi: 10.1103/PhysRevLett.87.133602 [89] de Oliveira AG, Arruda MFZ, Soares WC, Walborn SP, Khoury AZ et al. Phase conjugation and mode conversion in stimulated parametric down-conversion With orbital angular momentum: a geometrical interpretation. Braz J Phys 49, 10–16 (2019). doi: 10.1007/s13538-018-0614-4 [90] de Oliveira AG, Arruda MFZ, Soares WC, Walborn SP, Gomes RM et al. Real-time phase conjugation of vector vortex beams. ACS Photonics 7, 249–255 (2020). doi: 10.1021/acsphotonics.9b01524 [91] de Oliveira AG, da Silva NR, de Araújo RM, Ribeiro PHS, Walborn SP. Quantum optical description of phase conjugation of vector vortex beams in stimulated parametric down-conversion. Phys Rev Appl 14, 024048 (2020). doi: 10.1103/PhysRevApplied.14.024048 [92] da Silva NR, de Oliveira AG, Arruda MFZ, de Araújo RM, Soares WC et al. Stimulated parametric down-conversion With vector vortex beams. Phys Rev Appl 15, 024039 (2021). doi: 10.1103/PhysRevApplied.15.024039 [93] Brenier A. Investigation of the sum of orbital angular momentum generated by conical diffraction. J Opt 22, 045603 (2020). doi: 10.1088/2040-8986/ab76a7 [94] Yu HH, Zhang HJ, Wang ZP, Wang JY, Pan ZB et al. Experimental observation of optical vortex in self-frequency-doubling generation. Appl Phys Lett 99, 241102 (2011). doi: 10.1063/1.3670351 [95] Zolotovskaya SA, Abdolvand A, Kalkandjiev TK, Rafailov EU. Second-harmonic conical refraction: observation of free and forced harmonic Waves. Appl Phys B 103, 9–12 (2011). doi: 10.1007/s00340-011-4484-5 [96] Peet V, Shchemelyov S. Frequency doubling with laser beams transformed by conical refraction in a biaxial crystal. J Opt 13, 055205 (2011). doi: 10.1088/2040-8978/13/5/055205 [97] Tang YT, Li KF, Zhang XC, Deng JH, Li GX et al. Harmonic spin-orbit angular momentum cascade in nonlinear optical crystals. Nat Photonics 14, 658–662 (2020). doi: 10.1038/s41566-020-0691-0 [98] Forbes A. Structured light from lasers. Laser Photonics Rev 13, 1900140 (2019). doi: 10.1002/lpor.201900140 [99] Forbes A. Controlling light’s helicity at the source: orbital angular momentum states from lasers. Philos Trans A Math Phys Eng Sci 375, 20150436 (2017). [100] Omatsu T, Miyamoto K, Lee AJ. Wavelength-versatile optical vortex lasers. J Opt 19, 123002 (2017). doi: 10.1088/2040-8986/aa9445 [101] Naidoo D, Roux FS, Dudley A, Litvin I, Piccirillo B et al. Controlled generation of higher-order Poincaré sphere beams from a laser. Nat Photonics 10, 327–332 (2016). doi: 10.1038/nphoton.2016.37 [102] Wei DZ, Cheng Y, Ni R, Zhang Y, Hu XP et al. Generating controllable Laguerre-Gaussian laser modes through intracavity spin-orbital angular momentum conversion of light. Phys Rev Appl 11, 014038 (2019). doi: 10.1103/PhysRevApplied.11.014038 [103] Yusufu T, Niu SJ, Tuersun P, Tulake Y, Miyamoto K et al. Tunable 3 μm optical vortex parametric oscillator. Jpn J Appl Phys 57, 122701 (2018). doi: 10.7567/JJAP.57.122701 [104] Zhou N, Liu J, Wang J. Reconfigurable and tunable twisted light laser. Sci Rep 8, 11394 (2018). doi: 10.1038/s41598-018-29868-8 [105] Sroor H, Lisa N, Naidoo D, Litvin I, Forbes A. Cylindrical vector beams through amplifiers. Proc SPIE 10511, 105111M (2018). [106] Ahmed MA, Beirow F, Loescher A, Dietrich T, Bashir D et al. High-power thin-disk lasers emitting beams with axially-symmetric polarizations. Nanophotonics 11, 835–846 (2022). doi: 10.1515/nanoph-2021-0606 [107] Zhong HZ, Liang CC, Dai SY, Huang JF, Hu SS et al. Polarization-insensitive, high-gain parametric amplification of radially polarized femtosecond pulses. Optica 8, 62–69 (2021). doi: 10.1364/OPTICA.413328 [108] Jung Y, Kang QY, Sidharthan R, Ho D, Yoo S et al. Optical orbital angular momentum amplifier based on an air-hole erbium-doped fiber. J Lightwave Technol 35, 430–436 (2017). doi: 10.1109/JLT.2017.2651145 [109] Zhu S, Pidishety S, Feng YT, Hong S, Demas J et al. Multimode-pumped Raman amplification of a higher order mode in a large mode area fiber. Opt Express 26, 23295–23304 (2018). doi: 10.1364/OE.26.023295 [110] Bell T, Kgomo M, Ngcobo S. Digital laser for on-demand intracavity selective excitation of second harmonic higher-order modes. Opt Express 28, 16907–16923 (2020). doi: 10.1364/OE.385569 [111] Sroor H, Huang YW, Sephton B, Naidoo D, Vallés A et al. High-purity orbital angular momentum states from a visible metasurface laser. Nat Photonics 14, 498–503 (2020). doi: 10.1038/s41566-020-0623-z [112] Rao AS, Miike T, Miyamoto K, Omatsu T. Optical vortex lattice mode generation from a diode-pumped Pr3+: LiYF4 laser. J Opt 23, 075502 (2021). doi: 10.1088/2040-8986/ac067d [113] Rao AS, Miamoto K, Omatsu T. Ultraviolet intracavity frequency-doubled Pr3+: LiYF4 orbital Poincaré laser. Opt Express 28, 37397–37405 (2020). doi: 10.1364/OE.411624 [114] Vaupel M, Maître A, Fabre C. Observation of pattern formation in optical parametric oscillators. Phys Rev Lett 83, 5278–5281 (1999). doi: 10.1103/PhysRevLett.83.5278 [115] Marte M, Ritsch H, Petsas KI, Gatti A, Lugiato LA et al. Spatial patterns in optical parametric oscillators with spherical mirrors: classical and quantum effects. Opt Express 3, 71–80 (1998). doi: 10.1364/OE.3.000071 [116] Ducci S, Treps N, Maître A, Fabre C. Pattern formation in optical parametric oscillators. Phys Rev A 64, 023803 (2001). doi: 10.1103/PhysRevA.64.023803 [117] Lassen M, Delaubert V, Janousek J, Wagner K, Bachor HA et al. Tools for multimode quantum information: modulation, detection, and spatial quantum correlations. Phys Rev Lett 98, 083602 (2007). doi: 10.1103/PhysRevLett.98.083602 [118] Martinelli M, Huguenin JAO, Nussenzveig P, Khoury AZ. Orbital angular momentum exchange in an optical parametric oscillator. Phys Rev A 70, 013812 (2004). doi: 10.1103/PhysRevA.70.013812 [119] Barros RF, Alves GB, Tasca DS, Souza CER, Khoury AZ. Fine-tuning of orbital angular momentum in an optical parametric oscillator. J Phys B At Mol Opt Phys 52, 244002 (2019). doi: 10.1088/1361-6455/ab4cc8 [120] Qi T, Wang DM, Gao W. Sum-frequency generation of ring-airy beams. Appl Phys B 128, 67 (2022). [121] Dolev I, Ellenbogen T, Arie A. Switching the acceleration direction of airy beams by a nonlinear optical process. Opt Lett 35, 1581–1583 (2010). doi: 10.1364/OL.35.001581 [122] Ni R, Niu YF, Du L, Hu XP, Zhang Y et al. Topological charge transfer in frequency doubling of fractional orbital angular momentum state. Appl Phys Lett 109, 151103 (2016). doi: 10.1063/1.4964712 [123] Dmitriev VG, Gurzadyan GG, Nikogosyan DN. Handbook of Nonlinear Optical Crystals 2nd ed (Springer, Berlin, 1997). [124] Berger V. Nonlinear photonic crystals. Phys Rev Lett 81, 4136–4139 (1998). doi: 10.1103/PhysRevLett.81.4136 [125] Saltiel S, Kivshar YS. Phase matching in nonlinear χ(2) photonic crystals. Opt Lett 25, 1204–1206 (2000). doi: 10.1364/OL.25.001204 [126] Arie A, Voloch N. Periodic, quasi-periodic, and random quadratic nonlinear photonic crystals. Laser Photonics Rev 4, 355–373 (2010). doi: 10.1002/lpor.200910006 [127] Zhang Y, Wen JM, Zhu SN, Xiao M. Nonlinear Talbot effect. Phys Rev Lett 104, 183901 (2010). doi: 10.1103/PhysRevLett.104.183901 [128] Shapira A, Juwiler I, Arie A. Nonlinear computer-generated holograms. Opt Letters 36, 3015–3017 (2011). doi: 10.1364/OL.36.003015 [129] Shapira A, Shiloh R, Juwiler I, Arie A. Two-dimensional nonlinear beam shaping. Opt Lett 37, 2136–2138 (2012). doi: 10.1364/OL.37.002136 [130] Bloch NV, Shemer K, Shapira A, Shiloh R, Juwiler I et al. Twisting light by nonlinear photonic crystals. Phys Rev Lett 108, 233902 (2012). doi: 10.1103/PhysRevLett.108.233902 [131] Shiloh R, Arie A. Spectral and temporal holograms with nonlinear optics. Opt Lett 37, 3591–3593 (2012). doi: 10.1364/OL.37.003591 [132] Leshem A, Shiloh R, Arie A. Experimental realization of spectral shaping using nonlinear optical holograms. Opt Lett 39, 5370–5373 (2014). doi: 10.1364/OL.39.005370 [133] Chen PC, Wang CW, Wei DZ, Hu YL, Xu XY et al. Quasi-phase-matching-division multiplexing holography in a three-dimensional nonlinear photonic crystal. Light Sci Appl 10, 146 (2021). doi: 10.1038/s41377-021-00588-5 [134] Lou YC, Cheng ZM, Liu ZH, Yang YX, Ren ZC et al. Third-harmonic generation of spatially structured light in a quasi-periodically poled crystal. Optica 9, 183–186 (2022). doi: 10.1364/OPTICA.449590 [135] Chen Y, Ni R, Wu YD, Du L, Hu XP et al. Phase-matching controlled orbital angular momentum conversion in periodically poled crystals. Phys Rev Lett 125, 143901 (2020). doi: 10.1103/PhysRevLett.125.143901 [136] Wei DZ, Wang CW, Wang HJ, Hu XP, Wei D et al. Experimental demonstration of a three-dimensional lithium niobate nonlinear photonic crystal. Nat Photonics 12, 596–600 (2018). doi: 10.1038/s41566-018-0240-2 [137] Keren-Zur S, Ellenbogen T. A new dimension for nonlinear photonic crystals. Nat Photonics 12, 575–577 (2018). doi: 10.1038/s41566-018-0262-9 [138] Wei DZ, Wang CW, Xu XY, Wang HJ, Hu YL et al. Efficient nonlinear beam shaping in three-dimensional lithium niobate nonlinear photonic crystals. Nat Communications 10, 4193 (2019). doi: 10.1038/s41467-019-12251-0 [139] Zhang Y, Sheng Y, Zhu SN, Xiao M, Krolikowski W. Nonlinear photonic crystals: from 2D to 3D. Optica 8, 372–381 (2021). doi: 10.1364/OPTICA.416619 [140] Lee HJ, Kim H, Cha M, Moon HS. Simultaneous type-0 and type-II spontaneous parametric downconversions in a single periodically poled KTiOPO4 crystal. Appl Phys B 108, 585–589 (2012). doi: 10.1007/s00340-012-5088-4 [141] Zhang WG, Yu HW, Wu HP, Halasyamani PS. Phase-matching in nonlinear optical compounds: a materials perspective. Chem Mater 29, 2655–2668 (2017). doi: 10.1021/acs.chemmater.7b00243 [142] Jáuregui R, Torres JP. On the use of structured light in nonlinear optics studies of the symmetry group of a crystal. Sci Repo 6, 20906 (2016). doi: 10.1038/srep20906 [143] Chen SM, Li KF, Deng JH, Li GX, Zhang S. High-order nonlinear spin-orbit interaction on plasmonic metasurfaces. Nano Lett 20, 8549–8555 (2020). doi: 10.1021/acs.nanolett.0c03100 [144] Schlickriede C, Kruk SS, Wang L, Sain B, Kivshar Y et al. Nonlinear imaging with all-dielectric metasurfaces. Nano Lett 20, 4370–4376 (2020). doi: 10.1021/acs.nanolett.0c01105 [145] Rahmani M, Leo G, Brener I, Zayats AV, Maier SA et al. Nonlinear frequency conversion in optical nanoantennas and metasurfaces: materials evolution and fabrication. Opto-Electron Adv 1, 180021 (2018). [146] Zhang YB, Liu H, Cheng H, Tian JG, Chen SQ. Multidimensional manipulation of wave fields based on artificial microstructures. Opto-Electron Adv 3, 200002 (2020). doi: 10.29026/oea.2020.200002 [147] Pertsch T, Kivshar Y. Nonlinear optics with resonant metasurfaces. MRS Bull 45, 210–220 (2020). doi: 10.1557/mrs.2020.65 [148] Grinblat G. Nonlinear dielectric nanoantennas and metasurfaces: frequency conversion and wavefront control. ACS Photonics 8, 3406–3432 (2021). doi: 10.1021/acsphotonics.1c01356 [149] Wang L, Kruk S, Koshelev K, Kravchenko I, Luther-Davies B et al. Nonlinear wavefront control with all-dielectric metasurfaces. Nano Lett 18, 3978–3984 (2018). doi: 10.1021/acs.nanolett.8b01460 [150] Li GX, Chen SM, Pholchai N, Reineke B, Wong PWH et al. Continuous control of the nonlinearity phase for harmonic generations. Nat Mater 14, 607–612 (2015). doi: 10.1038/nmat4267 [151] Gao YS, Fan YB, Wang YJ, Yang WH, Song QH et al. Nonlinear holographic all-dielectric metasurfaces. Nano Lett 18, 8054–8061 (2018). doi: 10.1021/acs.nanolett.8b04311 [152] Li GX, Wu L, Li KF, Chen SM, Schlickriede C et al. Nonlinear metasurface for simultaneous control of spin and orbital angular momentum in second harmonic generation. Nano Lett 17, 7974–7979 (2017). doi: 10.1021/acs.nanolett.7b04451 [153] Walter F, Li GX, Meier C, Zhang S, Zentgraf T. Ultrathin nonlinear metasurface for optical image encoding. Nano Lett 17, 3171–3175 (2017). doi: 10.1021/acs.nanolett.7b00676 [154] Chen SM, Reineke B, Li GX, Zentgraf T, Zhang S. Strong nonlinear optical activity induced by lattice surface modes on Plasmonic metasurface. Nano Lett 19, 6278–6283 (2019). doi: 10.1021/acs.nanolett.9b02417 [155] Yariv A. Four wave nonlinear optical mixing as real time holography. Opt Commun 25, 23–25 (1978). doi: 10.1016/0030-4018(78)90079-2 [156] Liu HG, Li J, Fang XL, Zhao XH, Zheng YL et al. Dynamic computer-generated nonlinear-optical holograms. Phys Rev A 96, 023801 (2017). doi: 10.1103/PhysRevA.96.023801 [157] Qiu XD, Li FS, Liu HG, Chen XF, Chen LX. Optical vortex copier and regenerator in the Fourier domain. Photonics Res 6, 641–646 (2018). doi: 10.1364/PRJ.6.000641 [158] Liu HG, Zhao XH, Li H, Zheng YL, Chen XF. Dynamic computer-generated nonlinear optical holograms in a non-collinear second-harmonic generation Process. Opt Lett 43, 3236–3239 (2018). doi: 10.1364/OL.43.003236 [159] Liu S, Mazur LM, Krolikowski W, Sheng Y. Nonlinear volume holography in 3D nonlinear photonic crystals. Laser Photonics Rev 14, 2000224 (2020). doi: 10.1002/lpor.202000224 [160] Hong XH, Yang B, Zhang C, Qin YQ, Zhu YY. Nonlinear volume holography for wave-front engineering. Phys Rev Lett 113, 163902 (2014). doi: 10.1103/PhysRevLett.113.163902 [161] Trajtenebrg-Mills S, Arie A. Shaping light beams in nonlinear processes using structured light and patterned crystals. Opt Mater Express 7, 2928–2942 (2017). doi: 10.1364/OME.7.002928 [162] Shapira A, Naor L, Arie A. Nonlinear optical holograms for spatial and spectral shaping of light waves. Sci Bull 60, 1403–1415 (2015). doi: 10.1007/s11434-015-0855-3 [163] Liu HG, Chen XF. The manipulation of second-order nonlinear harmonic wave by structured material and structured light. J Nonlinear Opt Phys Mater 27, 1850047 (2018). doi: 10.1142/S0218863518500479 [164] Tabosa JWR, Petrov DV. Optical pumping of orbital angular momentum of light in cold cesium atoms. Phys Rev Lett 83, 4967–4970 (1999). doi: 10.1103/PhysRevLett.83.4967 [165] Barreiro S, Tabosa JWR, Torres JP, Deyanova Y, Torner L. Four-wave mixing of light beams with engineered orbital angular momentum in cold cesium atoms. Opt Lett 29, 1515–1517 (2004). doi: 10.1364/OL.29.001515 [166] Prajapati N, Super N, Lanning NR, Dowling JP, Novikova I. Optical angular momentum manipulations in a four-wave mixing process. Opt Lett 44, 739–742 (2019). doi: 10.1364/OL.44.000739 [167] Offer RF, Stulga D, Riis E, Franke-Arnold S, Arnold AS. Spiral bandwidth of four-wave mixing in Rb vapour. Commun Phys 1, 84 (2018). doi: 10.1038/s42005-018-0077-5 [168] Danaci O, Rios C, Glasser RT. All-optical mode conversion via spatially multimode four-wave mixing. New J Phys 18, 073032 (2016). doi: 10.1088/1367-2630/18/7/073032 [169] Knutson EM, Swaim JD, Wyllie S, Glasser RT. Optimal mode configuration for multiple phase-matched four-wave-mixing processes. Phys Rev A 98, 013828 (2018). doi: 10.1103/PhysRevA.98.013828 [170] Offer RF, Daffurn A, Riis E, Griffin PF, Arnold AS et al. Gouy phase-matched angular and radial mode conversion in four-wave mixing. Phys Rev A 103, L021502 (2021). doi: 10.1103/PhysRevA.103.L021502 [171] Swaim JD, Knutson EM, Danaci O, Glasser RT. Multimode four-wave mixing with a spatially structured pump. Opt Lett 43, 2716–2719 (2018). doi: 10.1364/OL.43.002716 [172] Hasan SB, Lederer F, Rockstuhl C. Nonlinear plasmonic antennas. Mater Today 17, 478–485 (2014). doi: 10.1016/j.mattod.2014.05.009 [173] Kauranen M, Zayats AV. Nonlinear plasmonics. Nat Photonics 6, 737–748 (2012). doi: 10.1038/nphoton.2012.244 [174] Grinblat G, Li Y, Nielsen MP, Oulton RF, Maier SA. Degenerate four-wave mixing in a multiresonant germanium nanodisk. ACS Photonics 4, 2144–2149 (2017). doi: 10.1021/acsphotonics.7b00631 [175] Corkum PB. Plasma perspective on strong field multiphoton ionization. Phys Rev Lett 71, 1994–1997 (1993). doi: 10.1103/PhysRevLett.71.1994 [176] Fleischer A, Kfir O, Diskin T, Sidorenko P, Cohen O. Spin angular momentum and tunable polarization in high-harmonic generation. Nat Photonics 8, 543–549 (2014). doi: 10.1038/nphoton.2014.108 [177] Huang PC, Hernández-García C, Huang JT, Huang PY, Lu CH et al. Polarization control of isolated high-harmonic pulses. Nat Photonics 12, 349–354 (2018). doi: 10.1038/s41566-018-0145-0 [178] Gariepy G, Leach J, Kim KT, Hammond TJ, Frumker E et al. Creating high-harmonic beams with controlled orbital angular momentum. Phys Rev Lett 113, 153901 (2014). doi: 10.1103/PhysRevLett.113.153901 [179] Gauthier D, Ribič PR, Adhikary G, Camper A, Chappuis C et al. Tunable orbital angular momentum in high-harmonic generation. Nat Commun 8, 14971 (2017). doi: 10.1038/ncomms14971 [180] Géneaux R, Chappuis C, Auguste T, Beaulieu S, Gorman TT et al. Radial index of Laguerre-Gaussian modes in high-order-harmonic generation. Phys Rev A 95, 051801 (2017). doi: 10.1103/PhysRevA.95.051801 [181] Chappuis C, Bresteau D, Auguste T, Gobert O, Ruchon T. High-order harmonic generation in an active grating. Phys Rev A 99, 033806 (2019). doi: 10.1103/PhysRevA.99.033806 [182] Hareli L, Lobachinsky L, Shoulga G, Eliezer Y, Michaeli L et al. On-the-fly control of high-harmonic generation using a structured pump beam. Phys Rev Lett 120, 183902 (2018). doi: 10.1103/PhysRevLett.120.183902 [183] Panagiotopoulos P, Papazoglou DG, Couairon A, Tzortzakis S. Sharply autofocused ring-Airy beams transforming into non-linear intense light bullets. Nat Commun 4, 2622 (2013). doi: 10.1038/ncomms3622 [184] Dorney KM, Rego L, Brooks NJ, Román JS, Liao CT et al. Controlling the polarization and vortex charge of attosecond high-harmonic beams via simultaneous spin-orbit momentum conservation. Nat Photonics 13, 123–130 (2019). doi: 10.1038/s41566-018-0304-3 [185] Kong F, Zhang C, Larocque H, Bouchard F, Li Z et al. Spin-constrained orbital-angular-momentum control in high-harmonic generation. Phys Rev Res 1, 032008 (2019). doi: 10.1103/PhysRevResearch.1.032008 [186] Géneaux R, Camper A, Auguste T, Gobert O, Caillat J et al. Synthesis and characterization of attosecond light vortices in the extreme ultraviolet. Nat Commun 7, 12583 (2016). doi: 10.1038/ncomms12583 [187] Rego L, Dorney KM, Brooks NJ, Nguyen QL, Liao CT et al. Generation of extreme-ultraviolet beams with time-varying orbital angular momentum. Science 364, eaaw9486 (2019). doi: 10.1126/science.aaw9486 [188] Barreiro S, Tabosa JWR. Generation of light carrying orbital angular momentum via induced coherence grating in cold atoms. Phys Rev Lett 90, 133001 (2003). doi: 10.1103/PhysRevLett.90.133001 [189] Pugatch R, Shuker M, Firstenberg O, Ron A, Davidson N. Topological stability of stored optical vortices. Phys Rev Lett 98, 203601 (2007). doi: 10.1103/PhysRevLett.98.203601 [190] Moretti D, Felinto D, Tabosa JWR. Collapses and revivals of stored orbital angular momentum of light in a cold-atom ensemble. Phys Rev A 79, 023825 (2009). doi: 10.1103/PhysRevA.79.023825 [191] de Almeida AJF, Barreiro S, Martins WS, de OliVeira RA, Felinto D et al. Storage of orbital angular momenta of light via coherent population oscillation. Opt Lett 40, 2545–2548 (2015). doi: 10.1364/OL.40.002545 [192] de Oliveira RA, Borba GC, Martins WS, Barreiro S, Felinto D et al. Nonlinear optical memory for manipulation of orbital angular momentum of light. Opt Lett 40, 4939–4942 (2015). doi: 10.1364/OL.40.004939 [193] Veissier L, Nicolas A, Giner L, Maxein D, Sheremet AS et al. Reversible optical memory for twisted photons. Opt Lett 38, 712–714 (2013). doi: 10.1364/OL.38.000712 [194] Sukhorukov AP, Yangirova VV. Spatio-temporal vortices: properties, generation and recording. Proc SPIE 5949, 594906 (2005). [195] Gui G, Brooks NJ, Kapteyn HC, Murnane MM, Liao CT. Second-harmonic generation and the conservation of spatiotemporal orbital angular momentum of light. Nat Photonics 15, 608–613 (2021). doi: 10.1038/s41566-021-00841-8 [196] Hancock SW, Zahedpour S, Milchberg HM. Second-harmonic generation of spatiotemporal optical vortices and conservation of orbital angular momentum. Optica 8, 594–597 (2021). doi: 10.1364/OPTICA.422743 [197] Desyatnikov AS, Kivshar YS, Torner L. Optical vortices and vortex solitons. Prog Opt 47, 291–391 (2005). [198] Kivshar YS, Pelinovsky DE. Self-focusing and transverse instabilities of solitary waves. Phys Rep 331, 117–195 (2000). doi: 10.1016/S0370-1573(99)00106-4 [199] Reyna AS, de Araújo CB. Spatial phase modulation due to quintic and septic nonlinearities in metal colloids. Opt Express 22, 22456–22469 (2014). doi: 10.1364/OE.22.022456 [200] Reyna AS, de Araújo CB. Nonlinearity management of photonic composites and observation of spatial-modulation instability due to quintic nonlinearity. Phys Rev A 89, 063803 (2014). doi: 10.1103/PhysRevA.89.063803 [201] Reyna AS, Jorge KC, de Araújo CB. Two-dimensional solitons in a quintic-septimal medium. Phys Rev A 90, 063835 (2014). doi: 10.1103/PhysRevA.90.063835 [202] Reyna AS, Malomed BA, de Araújo CB. Stability conditions for one-dimensional optical solitons in cubic-quintic-septimal media. Phys Rev A 92, 033810 (2015). doi: 10.1103/PhysRevA.92.033810 [203] Reyna AS, Bergmann E, Brevet PF, de Araújo CB. Nonlinear polarization instability in cubic-quintic plasmonic nanocomposites. Opt Express 25, 21049–21067 (2017). doi: 10.1364/OE.25.021049 [204] Reyna AS, Boudebs G, Malomed BA, de Araújo CB. Robust self-trapping of vortex beams in a saturable optical medium. Phys Rev A 93, 013840 (2016). doi: 10.1103/PhysRevA.93.013840 [205] Kivshar Y. Bending light at will. Nat Phys 2, 729–730 (2006). doi: 10.1038/nphys452 [206] Kivshar YS, Stegeman GI. Spatial optical solitons. Opt Photonics News 13, 59–63 (2002). [207] Chen ZG, Segev M, Christodoulides DN. Optical spatial solitons: historical overview and recent advances. Rep Prog Phys 75, 086401 (2012). doi: 10.1088/0034-4885/75/8/086401 [208] Reyna AS, de Araújo CB. High-order optical nonlinearities in plasmonic nanocomposites—a review. Adv Opt Photonics 9, 720–774 (2017). doi: 10.1364/AOP.9.000720 [209] Kong FQ, Zhang CM, Bouchard F, Li ZY, Brown GG et al. Controlling the orbital angular momentum of high harmonic vortices. Nat Commun 8, 14970 (2017). doi: 10.1038/ncomms14970 [210] Couteau C. Spontaneous parametric down-conversion. Contemp Phys 59, 291–304 (2018). doi: 10.1080/00107514.2018.1488463 [211] Romero J, Giovannini D, McLaren MG, Galvez EJ, Forbes A et al. Orbital angular momentum correlations with a phase-flipped Gaussian mode pump beam. J Opt 14, 085401 (2012). doi: 10.1088/2040-8978/14/8/085401 [212] Walborn SP, de Oliveira AN, Pádua S, Monken CH. Multimode hong-ou-mandel interference. Phys Rev Lett 90, 143601 (2003). doi: 10.1103/PhysRevLett.90.143601 [213] Yao AM. Angular momentum decomposition of entangled photons with an arbitrary pump. New J Phys 13, 053048 (2011). doi: 10.1088/1367-2630/13/5/053048 [214] Vicuña-Hernández V, Santiago JT, Jerónimo-Moreno Y, Ramírez-Alarcón R, Cruz-Ramírez H et al. Double transverse wave-vector correlations in photon pairs generated by spontaneous parametric down-conversion pumped by Bessel-Gauss beams. Phys Rev A 94, 063863 (2016). doi: 10.1103/PhysRevA.94.063863 [215] Torres JP, Deyanova Y, Torner L, Molina-Terriza G. Preparation of engineered two-photon entangled states for multidimensional quantum information. Phys Rev A 67, 052313 (2003). doi: 10.1103/PhysRevA.67.052313 [216] Khoury AZ, Ribeiro PHS, Dechoum K. Transfer of angular spectrum in parametric down-conversion with structured light. Phys Rev A 102, 033708 (2020). doi: 10.1103/PhysRevA.102.033708 [217] Hu XM, Zhang C, Guo Y, Wang FX, Xing WB et al. Pathways for entanglement-based quantum communication in the face of high noise. Phys Rev Lett 127, 110505 (2021). doi: 10.1103/PhysRevLett.127.110505 [218] Hu XM, Xing WB, Liu BH, Huang YF, Li CF et al. Efficient generation of high-dimensional entanglement through multipath down-conversion. Phys Rev Lett 125, 090503 (2020). doi: 10.1103/PhysRevLett.125.090503 [219] Baghdasaryan B, Fritzsche S. Enhanced entanglement from Ince-Gaussian pump beams in spontaneous parametric down-conversion. Phys. Rev. A 102, 052412 (2020). doi: 10.1103/PhysRevA.102.052412 [220] Liu SL, Zhang YW, Yang C, Liu SK, Ge Z et al. Increasing two-photon entangled dimensions by shaping input-beam profiles. Phys Rev A 101, 052324 (2020). doi: 10.1103/PhysRevA.101.052324 [221] Chen YY, Zhang WH, Zhang DK, Qiu XD, Chen LX. Coherent generation of the complete high-dimensional bell basis by adaptive pump modulation. Phys Rev Appl 14, 054069 (2020). doi: 10.1103/PhysRevApplied.14.054069 [222] van der Meer R, Renema JJ, Brecht B, Silberhorn C, Pinkse PWH. Optimizing spontaneous parametric down-conversion sources for boson sampling. Phys Rev A 101, 063821 (2020). doi: 10.1103/PhysRevA.101.063821 [223] Bornman N, Buono WT, Lovemore M, Forbes A. Optimal pump shaping for entanglement control in any countable basis. Adv Quantum Technol 4, 2100066 (2021). doi: 10.1002/qute.202100066 [224] Chang DE, Vuletić V, Lukin MD. Quantum nonlinear optics — photon by photon. Nat Photonics 8, 685–694 (2014). doi: 10.1038/nphoton.2014.192 [225] Guerreiro T, Martin A, Sanguinetti B, Pelc JS, Langrock C et al. Nonlinear interaction between Single Photons. Phys Rev Lett 113, 173601 (2014). doi: 10.1103/PhysRevLett.113.173601 [226] Molotkov SN. Quantum teleportation of a single-photon wave packet. Phys Lett A 245, 339–344 (1998). doi: 10.1016/S0375-9601(98)00423-X [227] Molotkov SN. Experimental scheme for quantum teleportation of a one-photon packet. J Exp Theor Phys Lett 68, 263–270 (1998). doi: 10.1134/1.567857 [228] Walborn SP, Monken CH, Pádua S, Ribeiro PHS. Spatial correlations in parametric down-conversion. Phys Rep 495, 87–139 (2010). doi: 10.1016/j.physrep.2010.06.003 [229] Humble TS. Spectral and spread-spectral teleportation. Phys Rev A 81, 062339 (2010). doi: 10.1103/PhysRevA.81.062339 [230] Kim YH, Kulik SP, Shih Y. Quantum teleportation of a polarization state with a complete bell state measurement. Phys Rev Lett 86, 1370–1373 (2001). doi: 10.1103/PhysRevLett.86.1370 [231] Sangouard N, Sanguinetti B, Curtz N, Gisin N, Thew R et al. Faithful entanglement swapping based on sum-frequency generation. Phys Rev Lett 106, 120403 (2011). doi: 10.1103/PhysRevLett.106.120403 [232] Gisin N, Pironio S, Sangouard N. Proposal for implementing device-independent quantum key distribution based on a heralded qubit amplifier. Phys Rev Lett 105, 070501 (2010). doi: 10.1103/PhysRevLett.105.070501 [233] Minář J, de Riedmatten H, Sangouard N. Quantum repeaters based on heralded qubit amplifiers. Phys Rev A 85, 032313 (2012). doi: 10.1103/PhysRevA.85.032313 [234] Sephton B, Vallés A, Nape I, Cox MA, Steinlechner F et al. High-dimensional spatial teleportation enabled by nonlinear optics. arXiv: 2111.13624, 2021. -
Access History
Article Metrics
-
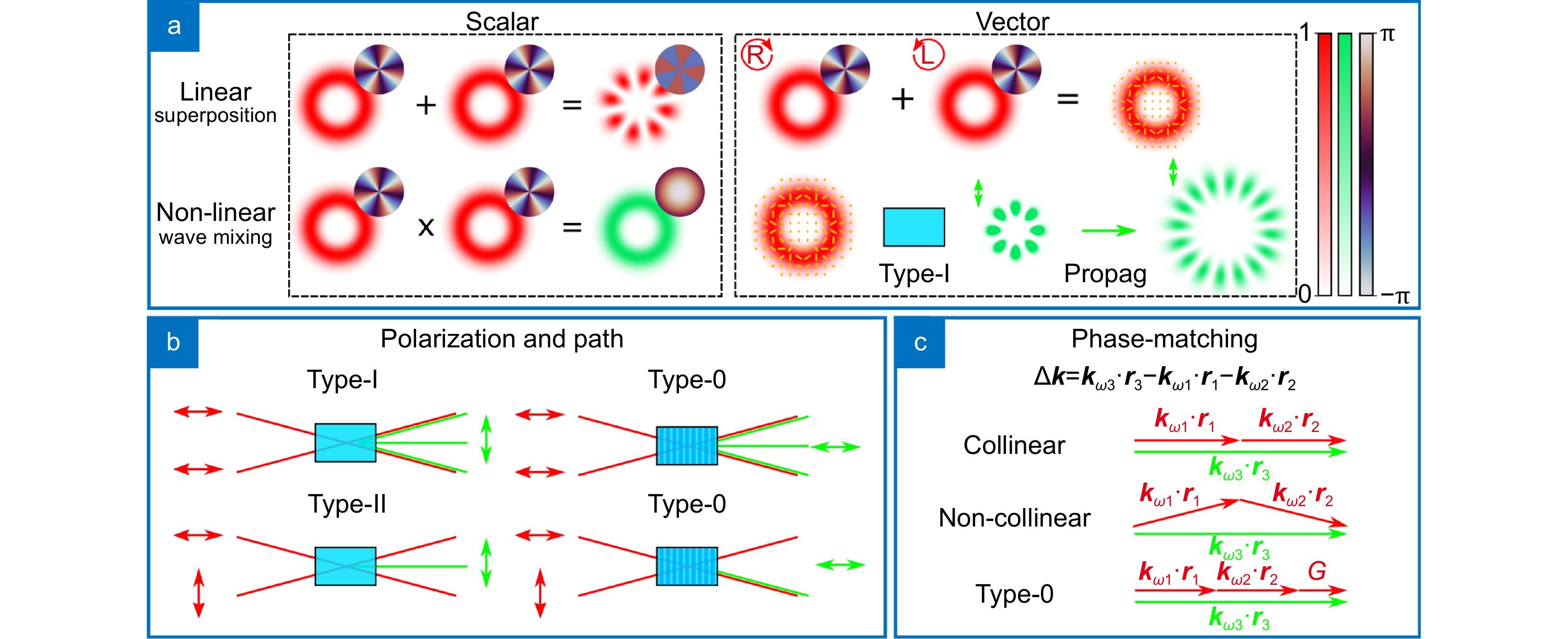
Figure 1.
Linear and nonlinear processes. Using second harmonic generation (SHG), we illustrate the differences between linear and nonlinear processes. (a) Linear processes produce an output mode that is the addition of two input spatial modes of light, while SHG produces the product of the two modes. The linear superposition of two different modes with orthogonal polarization states generates a vector beam, which has a inhomogeneous polarization state. The polarization profile is represented as yellow lines across the transverse profile. In SHG, and wave mixing in general, the polarization profile will dictate where wave mixing happens and thus alter directly the spatial profile. In (b) we show exemplify how path can also be controlled via polarization and the different phase matching conditions of crystals, including the periodic poling of type-0. The mechanism which allows these interactions is sketched in (c). Phase-matching is the condition necessary for wave mixing to occur and exploits birefringence (types I and II) or periodical polling (type-0) to achieve it.
-
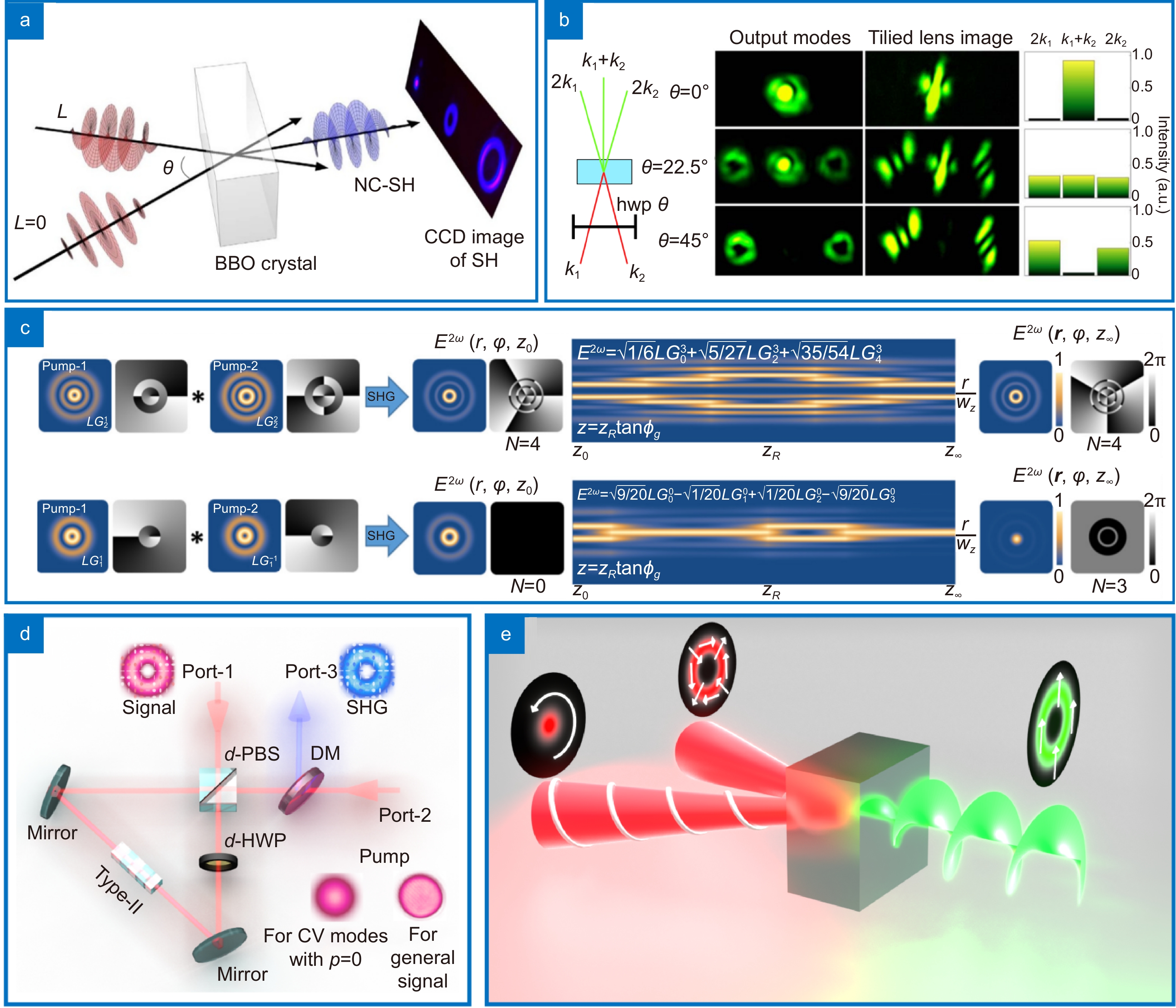
Figure 2.
Wave mixing with different degrees of freedom. In (a), the authors show OAM algebra in noncollinear SHG. When type-II phase-matching is used, the same noncollinear geometry allows for polarization switching, shown in (b). This effectively couples multiple degrees of freedom in a single process: path, polarization, radial and angular transverse structures. The radial selection rules of LG modes in wave mixing are demonstrated in (c). There is a intrinsic relation between the radial and angular degrees of freedom, which is manifested in the propagation dependence of the spatial profiles. In (d), a experimental scheme using a Sagnac interferometer achieves faithful frequency conversion of vector light. Spin and orbital angular momentum are combined in second harmonic generation in (e). Figure repoduced with permission from: (a) ref.48, Springer Nature; (b) ref.50, © Optica Publishing Group; (c) ref.54, © American Physical Society; (d) ref.69, American Physical Society; (e) ref.70, under aCreative Commons Attribution 4.0 International License
-
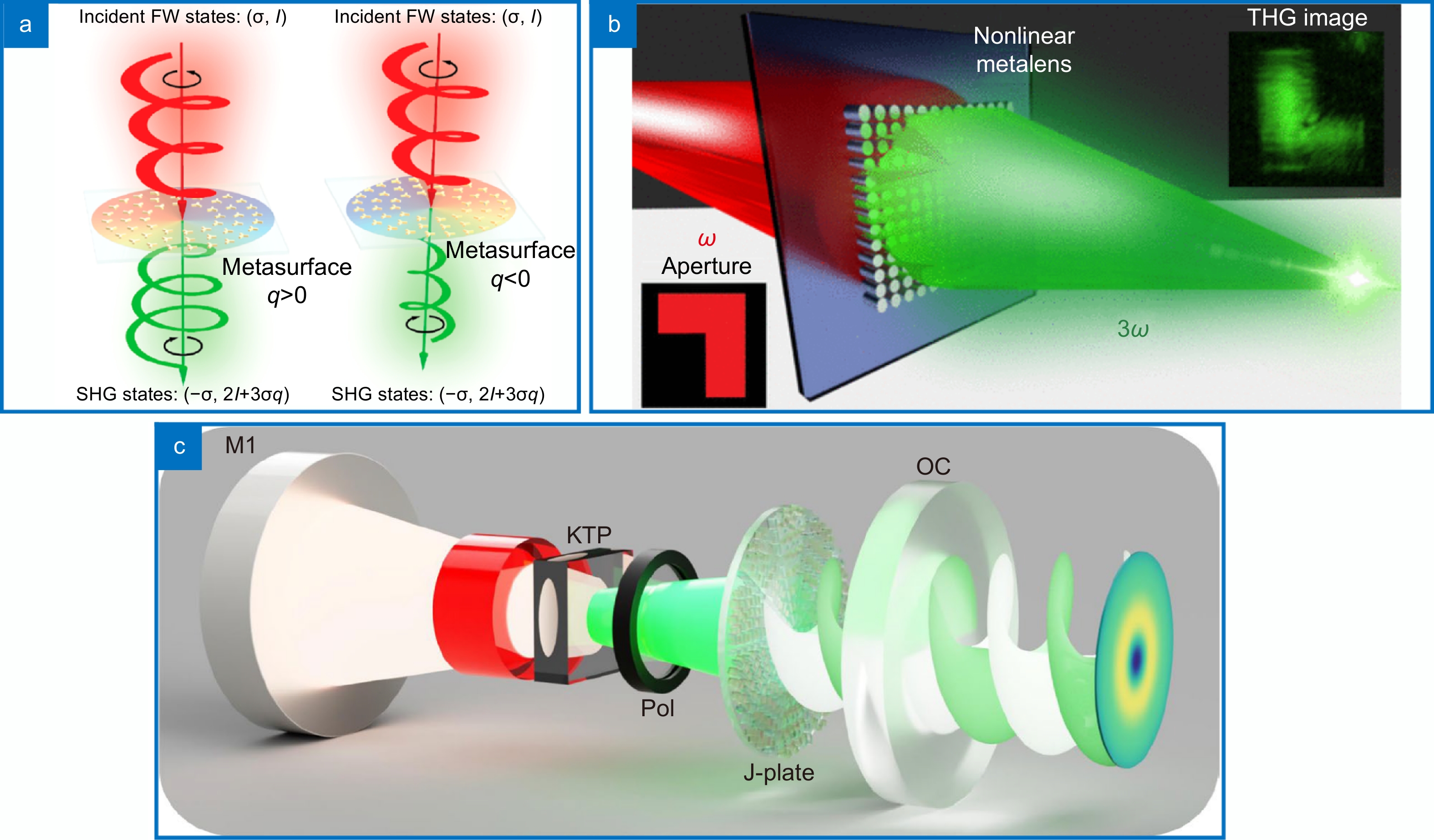
Figure 4.
Nonlinear optics enabled metasurfaces. These devices were shown to enable non-trivial interactions while frequency converting beams. In (a) a SHG process coupling SAM and OAM. The combination of frequency conversion with holography creates metasurfaces with metalensing properties in (b)144. An application taking advantage of the high damage threshold of these materials can be seen in (c)111 where the inclusion of a metasurface inside an optical cavity creates a laser with OAM from the source. Figure repoduced with permission from: (a) ref.143, © American Chemical Society; (b) ref.144, under a Creative Commons Non-Commercial No Derivative Works (CC-BY-NC-ND) Attribution License; (c) ref.111, Springer Nature.
-
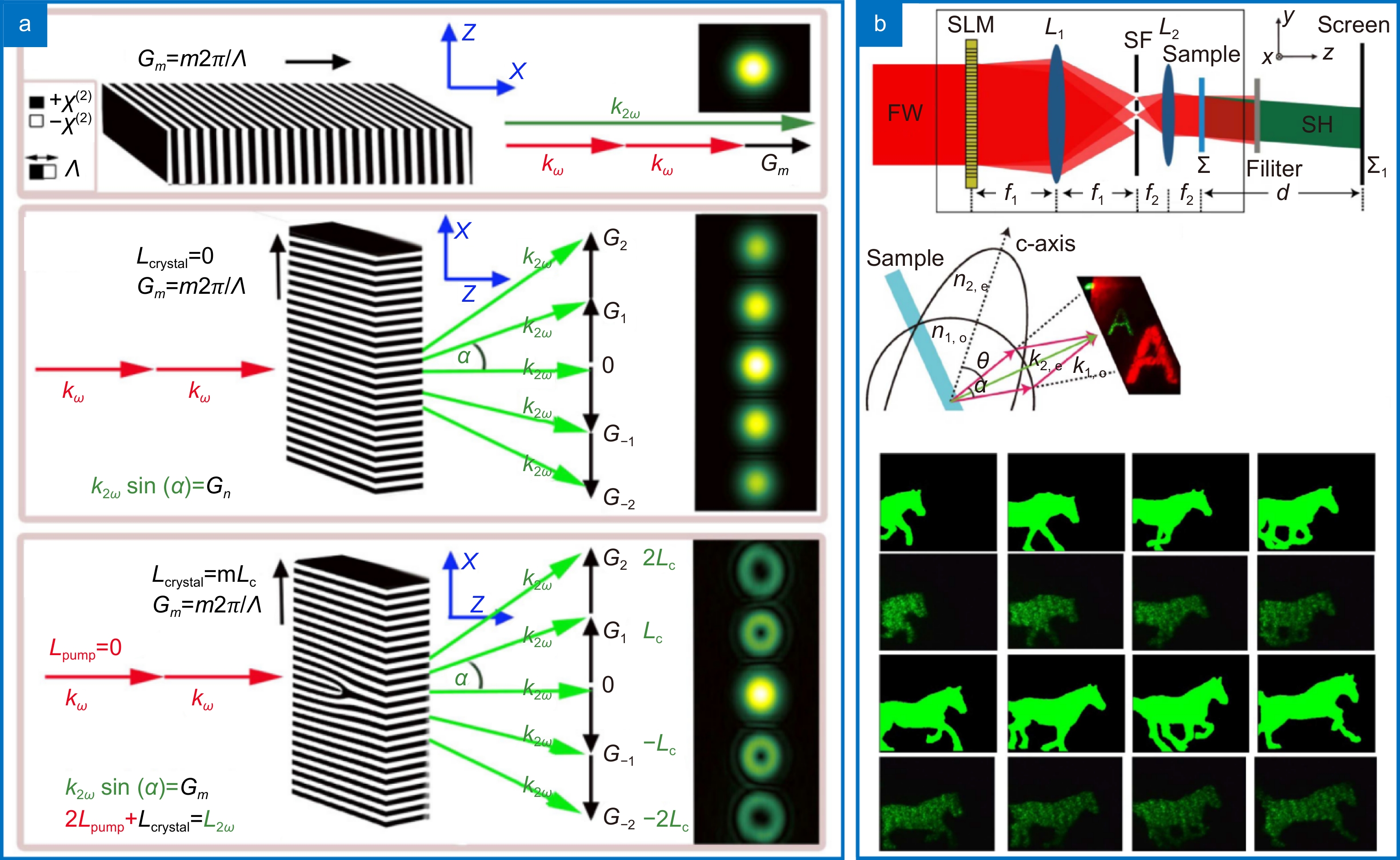
Figure 3.
Nonlinear Holography. In (a) the structuring of the medium is illustrated: the fundamental field is always the same, but the medium is not. The selective inversion of the electric domain across the transverse plane creates different spatial structures in the second harmonic field. The periodical transverse structure is responsible for multiple phase matching mechanisms, both longitudinally and transversely. In (b) it is shown how non-collinear SHG can transfer a specific intensity pattern from one wavelength to the other. First row shows the imaging arrangement and the second column shows the phase-matching conditions and an example of output modes. Right below is a experimental demonstration that this can be used for real-time frequency conversion of computer generated holograms. Figure repoduced from: (a) ref.130, © American Physical Society; (b) ref.158, © Optica Publishing Group.
-
Figure 5.
Higher order process. In the generation of high harmonic orders, it is possible to generate beams of many different OAM from just two different inputs, as depicted in (a). The process of writting and reading optical memory is depicted in (b) and the diference in time scales depending on the order of the nonlinear process in (c). In (d) it is demonstrated robust self-trapping of a bright vortex beam by exploiting higher order nonlinearities of odd orders. Figure repoduced from: (a) ref.209, Springer Nature; (b) ref.191, © Optica Publishing Group; (c) ref.192, © Optica Publishing Group; (d) ref.204, © American Physical Society.

 E-mail Alert
E-mail Alert RSS
RSS


 DownLoad:
DownLoad: