| Citation: | Zhu L, Zhao XS, Liu C, Fu SN, Wang YC et al. Flexible rotation of transverse optical field for 2D self-accelerating beams with a designated trajectory. Opto-Electron Adv 4, 200021 (2021).. doi: 10.29026/oea.2021.200021 |
Flexible rotation of transverse optical field for 2D self-accelerating beams with a designated trajectory
-
Abstract
Self-accelerating beams have the unusual ability to remain diffraction-free while undergo the transverse shift during the free-space propagation. We theoretically identify that the transverse optical field distribution of 2D self-accelerating beam is determined by the selection of the transverse Cartesian coordinates, when the caustic method is utilized for its trajectory design. Based on the coordinate-rotation method, we experimentally demonstrate a scheme to flexibly manipulate the rotation of transverse optical field for 2D self-accelerating beams under the condition of a designated trajectory. With this scheme, the transverse optical field can be rotated within a range of 90 degrees, especially when the trajectory of 2D self-accelerating beams needs to be maintained for free-space photonic interconnection.-
Keywords:
- self-accelerating beams /
- optical field /
- caustic
-
-
References
[1] Bandres MA, Kaminer I, Mills M, Rodríguez-Lara BM, Greenfield E et al. Accelerating optical beams. Opt Photonics News 24, 30–37 (2013). [2] Rosen J, Yariv A. Snake beam: a paraxial arbitrary focal line. Opt Lett 20, 2042–2044 (1995). doi: 10.1364/OL.20.002042 [3] Siviloglou GA, Broky J, Dogariu A, Christodoulides DN. Observation of accelerating Airy beams. Phys Rev Lett 99, 213901 (2007). doi: 10.1103/PhysRevLett.99.213901 [4] Siviloglou GA, Christodoulides DN. Accelerating finite energy Airy beams. Opt Lett 32, 979–981 (2007). doi: 10.1364/OL.32.000979 [5] Jia S, Vaughan JC, Zhuang XW. Isotropic three-dimensional super-resolution imaging with a self-bending point spread function. Nat Photonics 8, 302–306 (2014). doi: 10.1038/nphoton.2014.13 [6] Zhao JY, Chremmos ID, Song DH, Christodoulides DN, Efremidis NK et al. Curved singular beams for three-dimensional particle manipulation. Sci Rep 5, 12086 (2015). doi: 10.1038/srep12086 [7] Abdollahpour D, Suntsov S, Papazoglou DG, Tzortzakis S. Spatiotemporal airy light bullets in the linear and nonlinear regimes. Phys Rev Lett 105, 253901 (2010). doi: 10.1103/PhysRevLett.105.253901 [8] Chong A, Renninger WH, Christodoulides DN, Wise FW. Airy-Bessel wave packets as versatile linear light bullets. Nat Photonics 4, 103–106 (2010). doi: 10.1038/nphoton.2009.264 [9] Mathis A, Courvoisier F, Froehly L, Furfaro L, Jacquot M et al. Micromachining along a curve: Femtosecond laser micromachining of curved profiles in diamond and silicon using accelerating beams. Appl Phys Lett 101, 071110 (2012). doi: 10.1063/1.4745925 [10] Zhu GX, Wen YH, Wu X, Chen YJ, Liu L et al. Obstacle evasion in free-space optical communications utilizing Airy beams. Opt Lett 43, 1203–1206 (2018). doi: 10.1364/OL.43.001203 [11] Liang Y, Hu Y, Song DH, Lou CB, Zhang XZ et al. Image signal transmission with Airy beams. Opt Lett 40, 5686–5689 (2015). doi: 10.1364/OL.40.005686 [12] Bar-Ziv U, Postan A, Segev M. Observation of shape-preserving accelerating underwater acoustic beams. Phys Rev B 92, 100301 (2015). doi: 10.1103/PhysRevB.92.100301 [13] Voloch-Bloch N, Lereah Y, Lilach Y, Gover A, Arie A. Generation of electron Airy beams. Nature 494, 331–335 (2013). doi: 10.1038/nature11840 [14] Salandrino A, Christodoulides D. Airy plasmons defeat diffraction on the surface. Physics 4, 69 (2011). doi: 10.1103/Physics.4.69 [15] Zheng Y, Wu ZF, Shum PP, Xu ZL, Keiser G et al. Sensing and lasing applications of whispering gallery mode microresonators. Opto-Electron Adv 1, 180015 (2018). [16] Salandrino A, Christodoulides DN. Airy plasmon: a nondiffracting surface wave. Opt Lett 35, 2082–2084 (2010). doi: 10.1364/OL.35.002082 [17] Kaminer I, Bekenstein R, Nemirovsky J, Segev M. Nondiffracting accelerating wave packets of Maxwell’s equations. Phys Rev Lett 108, 163901 (2012). doi: 10.1103/PhysRevLett.108.163901 [18] Zhang P, Hu Y, Li TC, Cannan D, Yin XB et al. Nonparaxial Mathieu and weber accelerating beams. Phys Rev Lett 109, 193901 (2012). doi: 10.1103/PhysRevLett.109.193901 [19] Bandres MA, Rodríguez-Lara BM. Nondiffracting accelerating waves: weber waves and parabolic momentum. New J Phys 15, 013054 (2013). doi: 10.1088/1367-2630/15/1/013054 [20] Berry MV, Upstill C. IV Catastrophe optics: morphologies of caustics and their diffraction patterns. Prog Opt 18, 257–346 (1980). doi: 10.1016/S0079-6638(08)70215-4 [21] Vaveliuk P, Lencina A, Rodrigo JA, Matos OM. Caustics, catastrophes, and symmetries in curved beams. Phys Rev A 92, 033850 (2015). doi: 10.1103/PhysRevA.92.033850 [22] Greenfield E, Segev M, Walasik W, Raz O. Accelerating light beams along arbitrary convex trajectories. Phys Rev Lett 106, 213902 (2011). doi: 10.1103/PhysRevLett.106.213902 [23] Melamed T, Shlivinski A. Practical algorithm for custom-made caustic beams. Opt Lett 42, 2499–2502 (2017). doi: 10.1364/OL.42.002499 [24] Wen YH, Chen YJ, Zhang YF, Chen H, Yu SY. Winding light beams along elliptical helical trajectories. Phys Rev A 94, 013829 (2016). doi: 10.1103/PhysRevA.94.013829 [25] Guillemin V, Sternberg S. Geometric Asymptotics (American Mathematical Society, Providence, 1977). [26] Wen YH, Chen YJ, Zhang YF, Chen H, Yu SY. Tailoring accelerating beams in phase space. Phys Rev A 95, 023825 (2017). doi: 10.1103/PhysRevA.95.023825 [27] Bastiaans MJ. Application of the Wigner distribution function to partially coherent light. J Opt Soc Am A 3, 1227–1238 (2008). -
Access History
Article Metrics
-
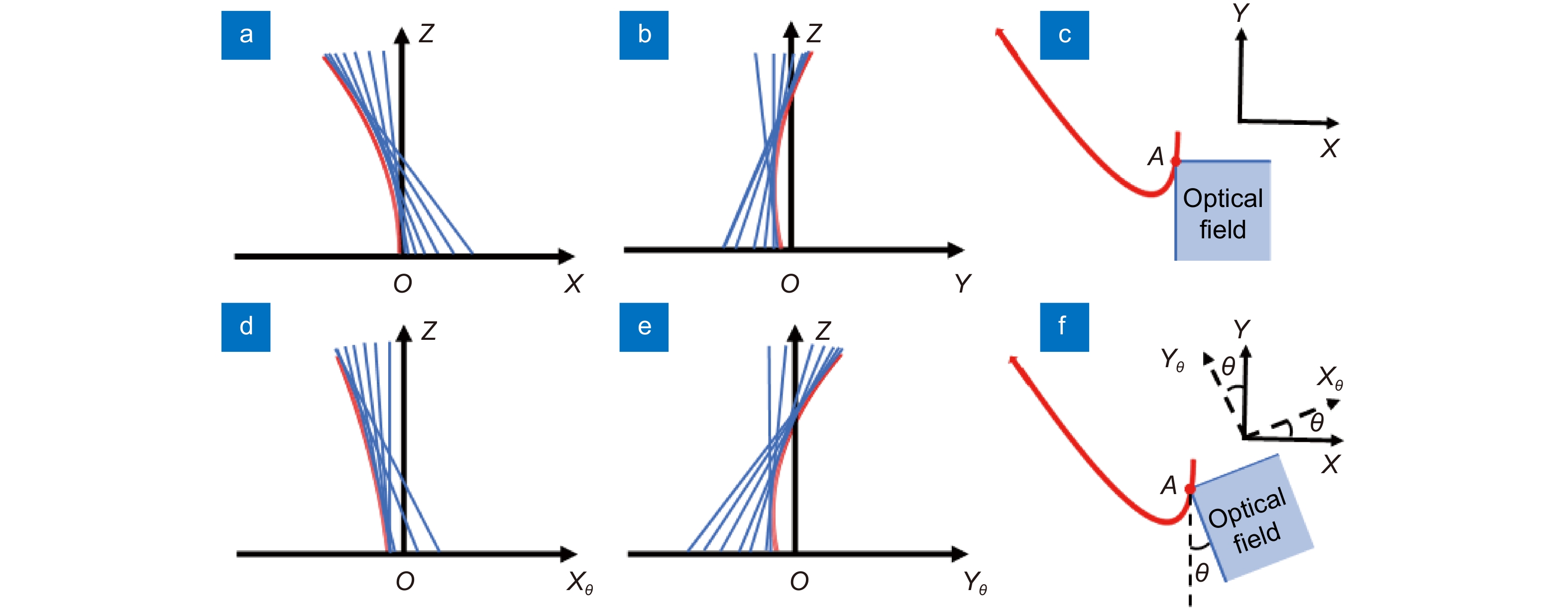
Figure 1.
Generation of 2D self-accelerating beam based on optical caustic and the rotation principle of transverse optical field for 2D self-accelerating beam. Two perpendicular components (a)−(b) of trajectory and light rays in default Cartesian coordinates. (c) The projection of multiplexed trajectory and the distribution of transverse optical field in default Cartesian coordinates; two perpendicular components (d)−(e) of trajectory and light rays in rotated Cartesian coordinates. (f) The projection of multiplexed trajectory and the rotated distribution of transverse optical field in rotated Cartesian coordinates.
-
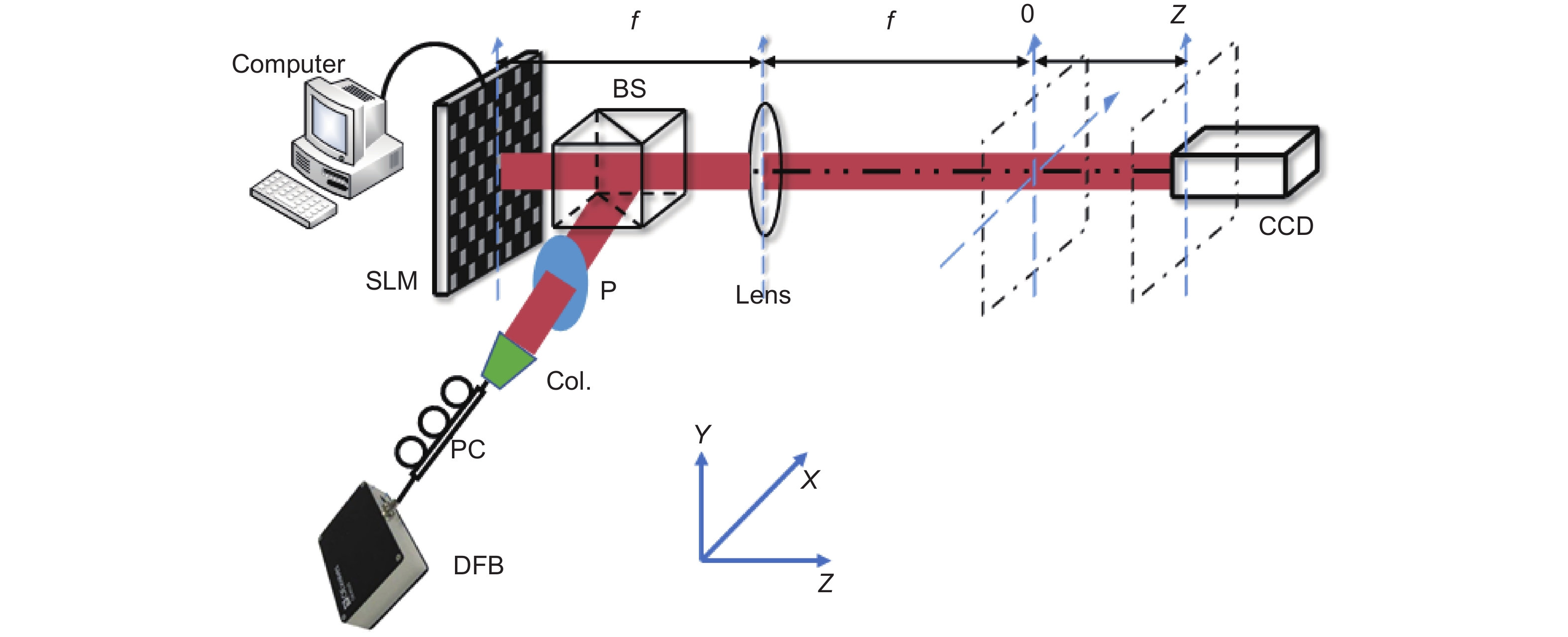
Figure 2.
Experimental setup for the optical field rotation of 2D self-accelerating beams. DFB: distributed feedback laser; Col.: collimator; PC: polarizer controller; P: polarizer; BS: beam splitter; SLM: spatial light modulator.
-
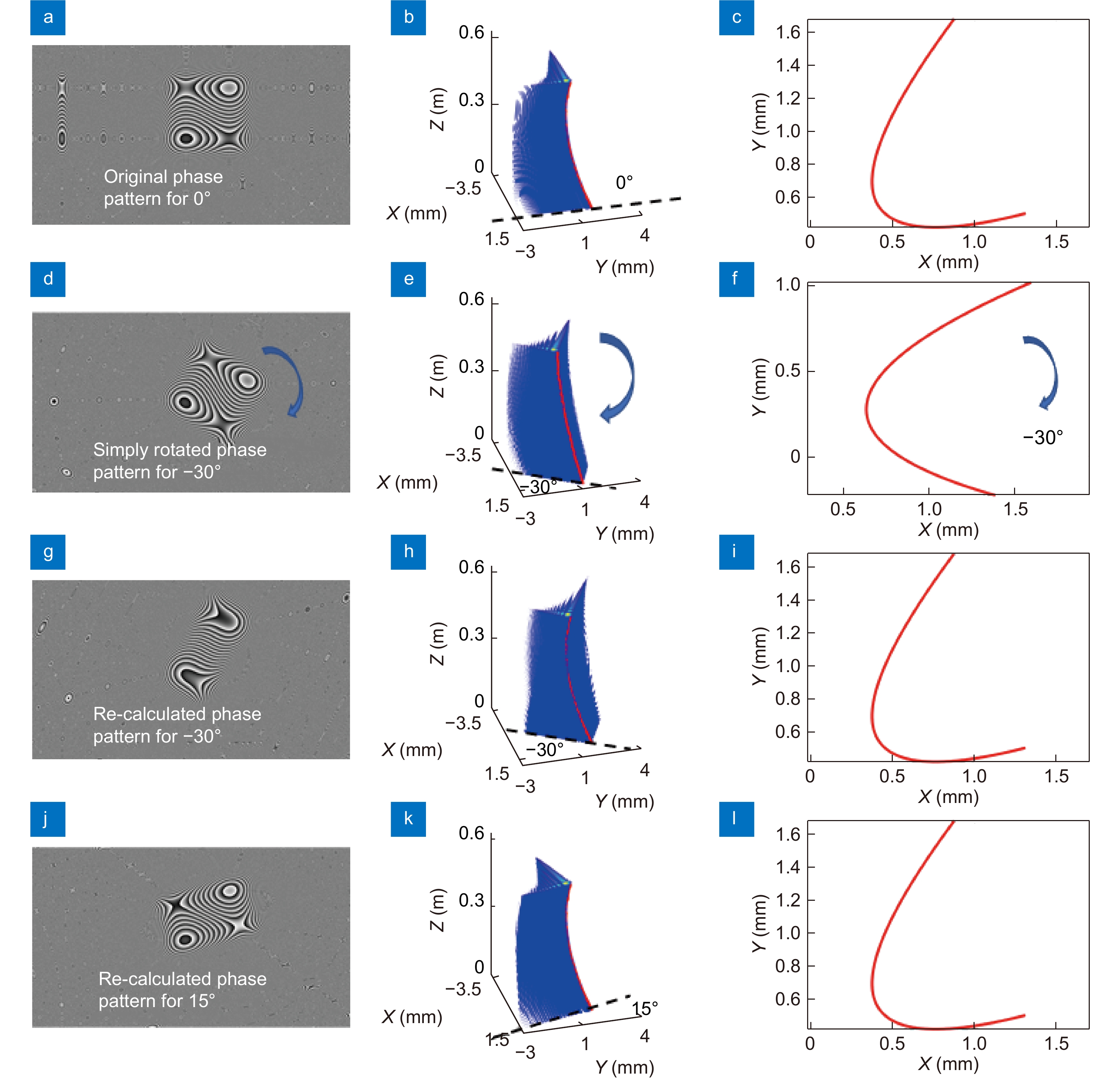
Figure 3.
Different phase patterns and their calculated 3D optical distribution and trajectories. (a) Original phase pattern and its (b) 3D optical distribution and (c) the projection of trajectory. (d) Simply rotated phase pattern for -30° and corresponding (e) 3D optical distribution and (f) the projection of trajectory. (g), (j) Re-calculated phase patterns for -30° and 15°, and (h), (k) their 3D optical distribution and (i), (l) the projection of trajectory.
-
Figure 4.
Calculated and experimental results for the optical field rotation of 2D Airy beam at different propagation distances. (a − c) Calculated phase patterns. (d − f), (j − l), (p − r) Simulated and (g − i), (m − o), (s − u) experimental intensity profiles at distance of 0, 0.3 m and 0.6 m with a rotation angle of -30°, 0° and 15°, respectively.
-
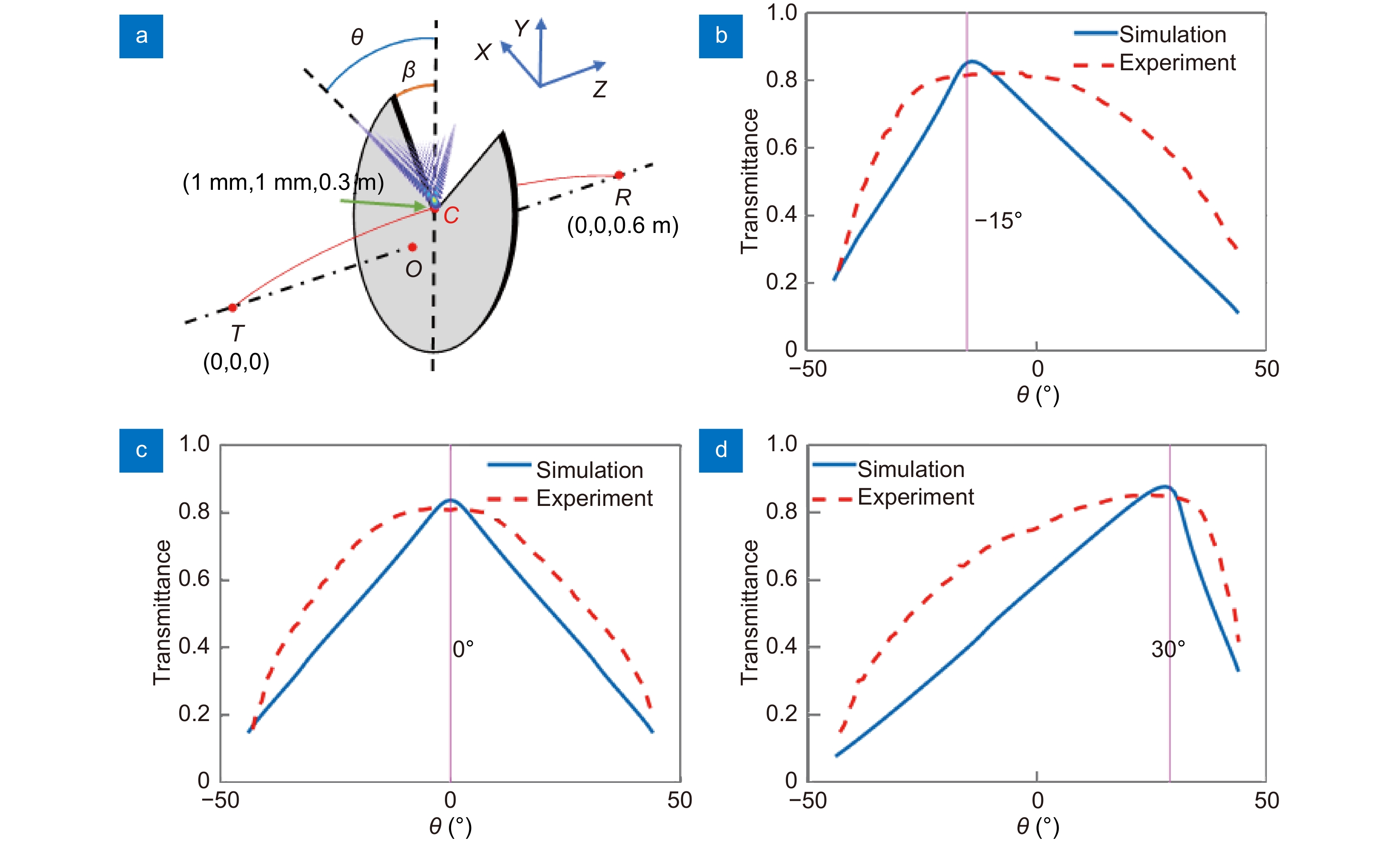
Figure 5.
Obstacle evasion experiment. (a) set-up; normalized received optical power with obstacle’s angle β of (b) -15° (c) 0° and (d) 30°. (blue solid curves are calculated results, and red dotted curves denote the experimental results.)

 E-mail Alert
E-mail Alert RSS
RSS


 DownLoad:
DownLoad: