E-mail Alert
RSS
| Citation: |
Chu CY, Liu ZT, Chen ML, Shao XH, Situ GH et al. Wide-spectrum optical synthetic aperture imaging via spatial intensity interferometry. Opto-Electron Adv 6, 230017 (2023). doi: 10.29026/oea.2023.230017
|
Article Open Access
Wide-spectrum optical synthetic aperture imaging via spatial intensity interferometry
-
Abstract
High resolution imaging is achieved using increasingly larger apertures and successively shorter wavelengths. Optical aperture synthesis is an important high-resolution imaging technology used in astronomy. Conventional long baseline amplitude interferometry is susceptible to uncontrollable phase fluctuations, and the technical difficulty increases rapidly as the wavelength decreases. The intensity interferometry inspired by HBT experiment is essentially insensitive to phase fluctuations, but suffers from a narrow spectral bandwidth which results in a lack of effective photons. In this study, we propose optical synthetic aperture imaging based on spatial intensity interferometry. This not only realizes diffraction-limited optical aperture synthesis in a single shot, but also enables imaging with a wide spectral bandwidth, which greatly improves the optical energy efficiency of intensity interferometry. And this method is insensitive to the optical path difference between the sub-apertures. Simulations and experiments present optical aperture synthesis diffraction-limited imaging through spatial intensity interferometry in a 100 nm spectral width of visible light, whose maximum optical path difference between the sub-apertures reaches 69λ. This technique is expected to provide a solution for optical aperture synthesis over kilometer-long baselines at optical wavelengths. -
-
References
[1] Brown RH, Twiss RQ. Correlation between photons in two coherent beams of light. Nature 177, 27–29 (1956). doi: 10.1038/177027a0 [2] Twiss RQ. Applications of intensity interferometry in physics and astronomy. Opt Acta Int J Opt 16, 423–451 (1969). doi: 10.1080/713818198 [3] Brown RH, Davis J, Allen LR. The angular diameters of 32 stars. Mon Not Roy Astron Soc 167, 121–136 (1974). doi: 10.1093/mnras/167.1.121 [4] Rivet JP, Vakili F, Lai O, Vernet D, Fouché M et al. Optical long baseline intensity interferometry: prospects for stellar physics. Exp Astron 46, 531–542 (2018). doi: 10.1007/s10686-018-9595-0 [5] Nuñez PD, Holmes R, Kieda D, LeBohec S. High angular resolution imaging with stellar intensity interferometry using air cherenkov telescope arrays. Mon Not Roy Astron Soc 419, 172–183 (2012). doi: 10.1111/j.1365-2966.2011.19683.x [6] Pilyavsky G, Mauskopf P, Smith N, Schroeder E, Sinclair A et al. Single-photon intensity interferometry (SPIIFy): utilizing available telescopes. Mon Not Roy Astron Soc 467, 3048–3055 (2017). doi: 10.1093/mnras/stx272 [7] Gori PM, Vakili F, Rivet JP, Guerin W, Hugbart M et al. I3T: intensity interferometry imaging telescope. Mon Not Roy Astron Soc 505, 2328–2335 (2021). doi: 10.1093/mnras/stab1424 [8] Xu BX, Fan XY, Wang S, He ZY. Sub-femtometer-resolution absolute spectroscopy with sweeping electro-optic combs. Opto-Electron Adv 5, 210023 (2022). doi: 10.29026/oea.2022.210023 [9] Li CL, Liu JC, Zhang FM Qu XH. Review of nonlinearity correction of frequency modulated continuous wave LiDAR measurement technology. Opto-Electron Eng 49, 210438 (2022). doi: 10.12086/oee.2022.210438 [10] Le Bohec S, Daniel M, de Wit WJ, Hinton JA, Jose E et al. Stellar intensity interferometry with air Cherenkov telescope arrays. AIP Conf Proc 984, 205–215 (20008). doi: 10.1063/1.2896931 [11] Dravins D, LeBohec S, Jensen H, Nuñez PD. Stellar intensity interferometry: prospects for sub-milliarcsecond optical imaging. New Astron Rev 56, 143–167 (2012). doi: 10.1016/j.newar.2012.06.001 [12] Buckley J, Coppi P, Digel S, Funk S, Krawczynski H et al. The Advanced Gamma‐ray Imaging System (AGIS)—Science Highlights. AIP Conf Proc 1085, 902–905 (2008). doi: 10.1063/1.3076823 [13] Gong WL, Han SS. High-resolution far-field ghost imaging via sparsity constraint. Sci Rep 5, 9280 (2015). doi: 10.1038/srep09280 [14] Bulbul A, Vijayakumar A, Rosen J. Superresolution far-field imaging by coded phase reflectors distributed only along the boundary of synthetic apertures. Optica 5, 1607–1616 (2018). doi: 10.1364/OPTICA.5.001607 [15] Liu ZT, Shen X, Liu HL, Yu H, Han SS. Lensless wiener–khinchin telescope based on second-order spatial autocorrelation of thermal light. Chin Opt Lett 17, 091101 (2019). doi: 10.3788/COL201917.091101 [16] Bulbul A, Rosen J. Super-resolution imaging by optical incoherent synthetic aperture with one channel at a time. Photonics Res 9, 1172–1181 (2021). doi: 10.1364/PRJ.422381 [17] Wang F, Wang CL, Chen ML, Gong WL, Zhang Y et al. Far-field super-resolution ghost imaging with a deep neural network constraint. Light Sci Appl 11, 1–11 (2022). doi: 10.1038/s41377-021-00680-w [18] Liu YL, Chen YH, Wang F, Cai YJ, Liang CH et al. Robust far-field imaging by spatial coherence engineering. Opto-Electron Adv 4, 210027 (2021). doi: 10.29026/oea.2021.210027 [19] Hu Y, Xiang HZ, Zhao RY, Tu JK, Zheng G. Mode field diameter measurement of single mode fiber using Bessel function fitting method based on variable aperture in far field. Opto-Electron Eng 48, 200308 (2021). doi: 10.12086/oee.2021.200308 [20] Liu ZT, Tan SY, Wu JR, Li ER, Shen X et al. Spectral camera based on ghost imaging via sparsity constraints. Sci Rep 6, 25718 (2016). doi: 10.1038/srep25718 [21] Chen SC, Du LH, Zhu LG. THz wave computational ghost imaging: principles and outlooks. Opto-Electron Eng 47, 200024 (2020). doi: 10.12086/oee.2020.200024 [22] Fienup JR. Reconstruction of an object from the modulus of its Fourier transform. Opt Lett 3, 27–29 (1978). doi: 10.1364/OL.3.000027 [23] Fienup JR. Phase retrieval algorithms: a comparison. Appl Opt 21, 2758–2769 (1982). doi: 10.1364/AO.21.002758 [24] Liu XL, Wu JC, He WQ, Liao MH, Zhang CG et al. Vulnerability to ciphertext-only attack of optical encryption scheme based on double random phase encoding. Opt Express 23, 18955–18968 (2015). doi: 10.1364/OE.23.018955 [25] Shechtman Y, Eldar YC, Cohen O, Chapman HN, Miao JW et al. Phase retrieval with application to optical imaging: a contemporary overview. IEEE Signal Process Mag 32, 87–109 (2015). doi: 10.1109/MSP.2014.2352673 [26] Sun J, Qu Q, Wright J. A geometric analysis of phase retrieval. Found Comput Math 18, 1131–1198 (2018). doi: 10.1007/s10208-017-9365-9 [27] Shen C, Liang MS, Pan A, Yang C. Non-iterative complex wave-field reconstruction based on Kramers–Kronig relations. Photonics Res 9, 1003–1012 (2021). doi: 10.1364/PRJ.419886 [28] Liao MH, Zheng SS, Pan SX, Lu DJ, He WQ et al. Deep-learning-based ciphertext-only attack on optical double random phase encryption. Opto-Electron Adv 4, 200016 (2021). doi: 10.29026/oea.2021.200016 [29] Feng SC, Kane C, Lee PA, Stone AD. Correlations and fluctuations of coherent wave transmission through disordered media. Phys Rev Lett 61, 834–837 (1988). doi: 10.1103/PhysRevLett.61.834 [30] Osnabrugge G, Horstmeyer R, Papadopoulos IN, Judkewitz B, Vellekoop IM. Generalized optical memory effect. Optica 4, 886–892 (2017). doi: 10.1364/OPTICA.4.000886 [31] Wang XY, Jin X, Li JQ. Blind position detection for large field-of-view scattering imaging. Photonics Res 8, 920–928 (2020). doi: 10.1364/PRJ.388522 [32] Goodman JW. Introduction to Fourier Optics 3rd ed 7–9 (Roberts & Company Publishers, Greenwoood Village, 2005). [33] Cohen L. The generalization of the wiener-khinchin theorem. in Proceedings of 1998 IEEE International Conference on Acoustics, Speech and Signal Processing 1577–1580 (IEEE, 1998). [34] Saha SK. Aperture Synthesis: Methods and Applications to Optical Astronomy 28 (Springer, New York, 2010). [35] Zheng GA, Shen C, Jiang SW, Song PM, Yang C. Concept, implementations and applications of Fourier ptychography. Nat Rev Phys 3, 207–223 (2021). doi: 10.1038/s42254-021-00280-y [36] Bashkansky M, Lucke RL, Funk E, Rickard LJ, Reintjes J. Two-dimensional synthetic aperture imaging in the optical domain. Opt Lett 27, 1983–1985 (2002). doi: 10.1364/OL.27.001983 [37] Derie F. VLTI delay lines: design, development, and performance requirements. Proc SPIE 40006, 25–40 (2000). doi: 10.1117/12.390216 [38] Shannon RR, Wyant JC. Applied Optics and Optical Engineering 156–158 (Academic Press, 1983). [39] Event Horizon Telescope Collaboration, Akiyama K, Alberdi A, Alef W, Algaba JC et al. First Sagittarius A* event horizon telescope results. I. The shadow of the supermassive black hole in the center of the milky way. Astrophys J Lett 930, L12 (2022). doi: 10.3847/2041-8213/ac6674 -
Supplementary Information
Supplementary information for Wide-spectrum optical synthetic aperture imaging via spatial intensity interferometry 
-
Access History
Figures(6)
Article Metrics
Export File
Citation
Chu CY, Liu ZT, Chen ML, Shao XH, Situ GH et al. Wide-spectrum optical synthetic aperture imaging via spatial intensity interferometry. Opto-Electron Adv 6, 230017 (2023). doi: 10.29026/oea.2023.230017
Format
Content
DownLoad:
-
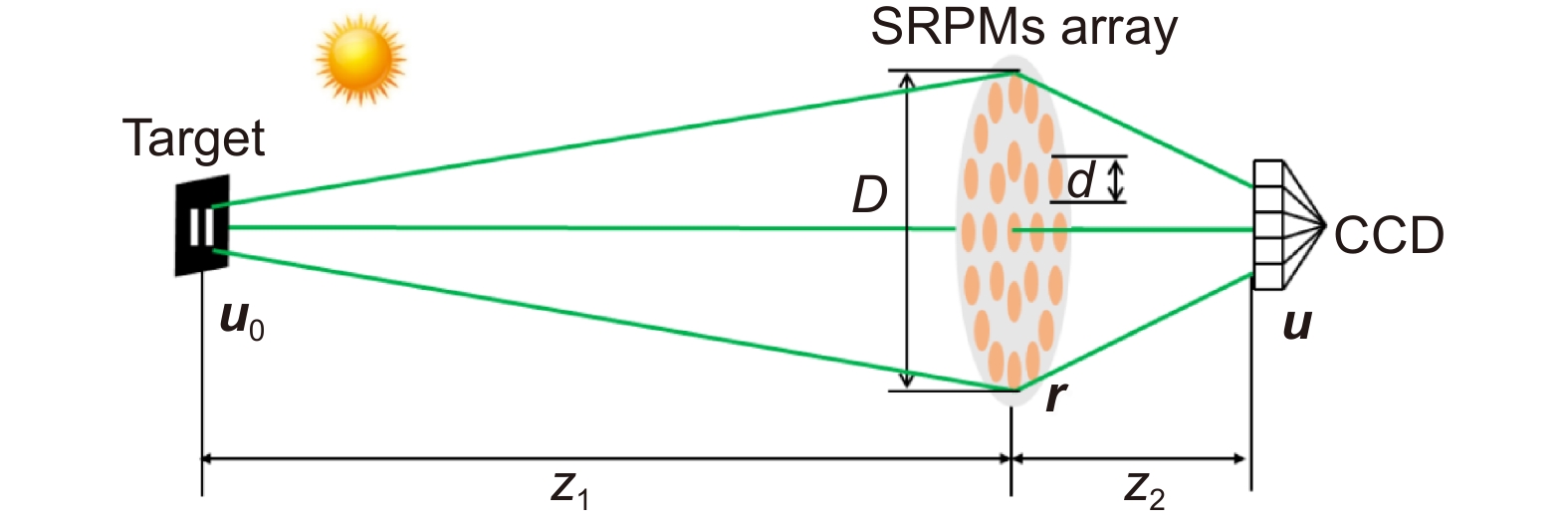
Figure 1.
Schematic of wide-spectrum optical synthetic aperture imaging via spatial intensity interferometry.
-
Figure 2.
(a) Traditional optical synthetic aperture system. (b) Schematic of wide-spectrum optical synthetic aperture imaging via spatial intensity interferometry.
-
Figure 3.
(a) Schematic diagram of the simulation structure. (b) Structure of sub-aperture SRPMs array. (c) Optical path structure of the experiment.
-
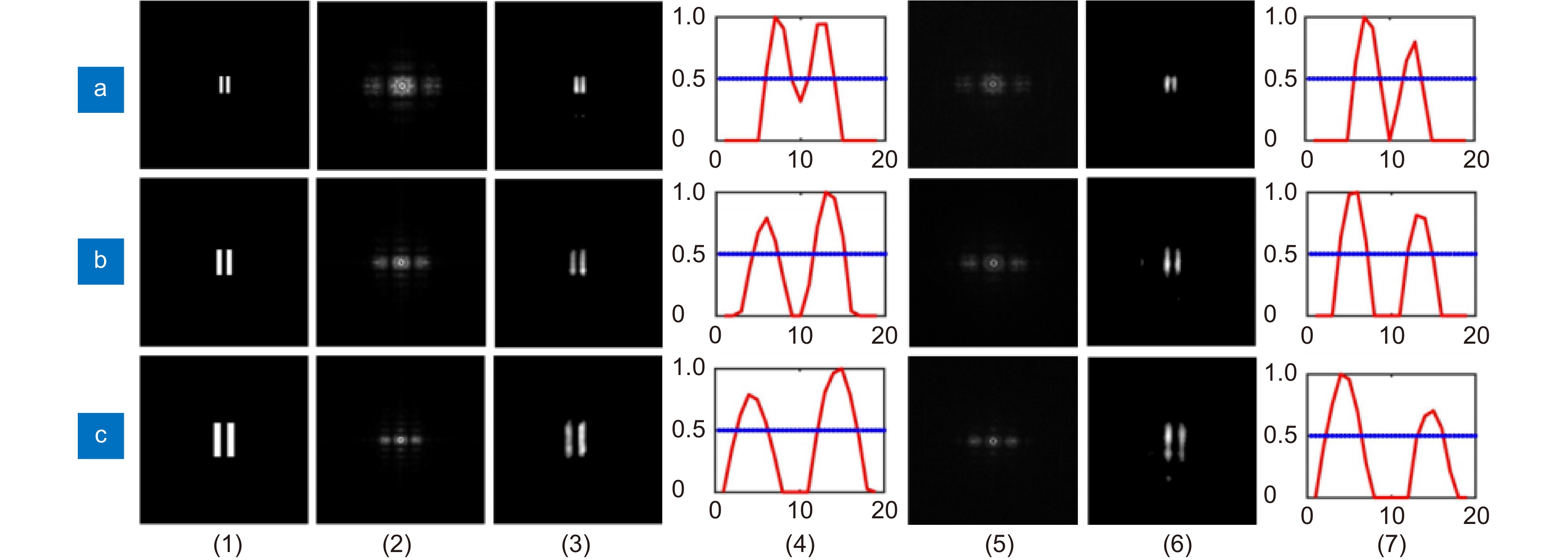
Figure 4.
Simulation and experimental results. The spectral widths of the filters were 532 ± 0.5 nm. (a1–c1) Targets. (2–4) Simulation results. (5–7) Experimental results. In the experiment, the exposure times of CCD were 1.2 s, 0.75 s, 0.5 s, and the gains of CCD were 30 dB, 30 dB, 28 dB, respectively. (2, 5) Spatial intensity autocorrelation of CCD. (3, 6) Reconstruction of target image using phase retrieval algorithms. (4, 7) One-dimensional normalized date of double slits reconstruction image. The blue lines indicate half of the maximum value.
-
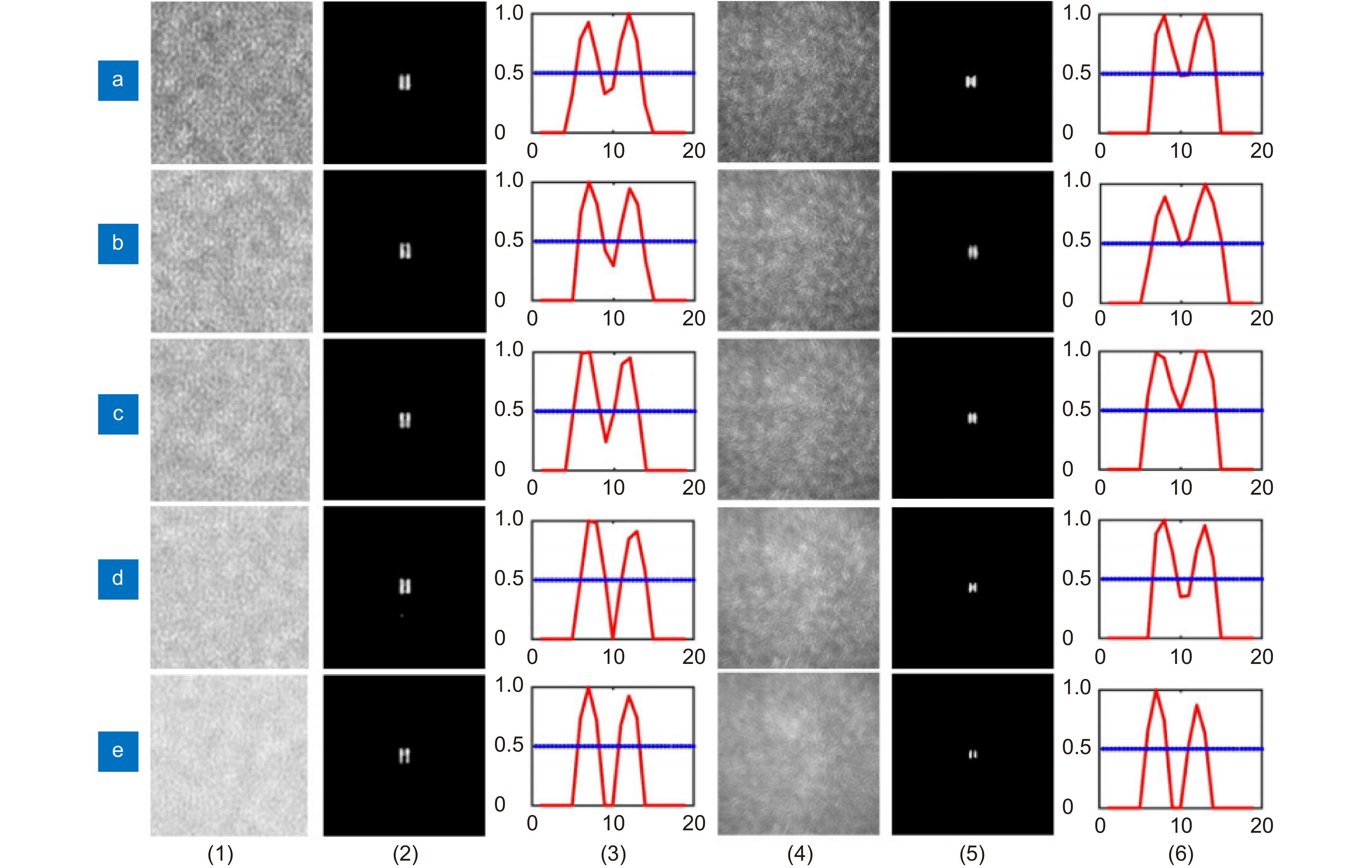
Figure 5.
Simulation and experimental results of wide-spectrum optical synthetic aperture imaging via spatial intensity interferometry. (a–e) The spectral ranges of the filters were 532 ±5 nm, ±10 nm, ±15 nm, ±25 nm, ±50 nm, respectively. (1–3) Simulation results. (4–6) Experimental results. The sampling exposure times of CCD were 250 ms, and the gains of CCD were 9 dB, 16 dB, 23 dB, 25 dB, 30 dB, respectively. (1, 4) The detected image by CCD. (2, 5) Reconstruction of target image using phase retrieval algorithms. (3, 6) One-dimensional normalized date of double slits reconstruction image. The blue lines indicate half of the maximum value.
-
Figure 6.
Experimental results of different sub-aperture SRPMS arrays. (a) Different sparse array structures. (b) Spatial intensity autocorrelation of different sparse array structures. (c1–c4) Reconstruction of ′s′ image using phase retrieval algorithms by different sparse array structures. (d1–d4) Reconstruction of double-slit image using phase retrieval algorithms by different sparse array structures. (5) Target letter ′s′ and double-slit, whose sizes were 2.0 mm and 0.98 mm, respectively.
