| Citation: | Liu YL, Dai ST, Zhu YM et al. Full-dimensional complex coherence properties tomography for multi-cipher information security. Opto-Electron Adv 8, 240278 (2025). doi: 10.29026/oea.2025.240278 |
Full-dimensional complex coherence properties tomography for multi-cipher information security
-
Abstract
Optical coherence is a fundamental property of light, playing a key role in understanding interference, propagation, and light-matter interactions for both classical and quantum light. Measuring the coherence properties of an optical field is crucial for a wide range of applications. However, despite many proposed measurement schemes, significant challenges still remain. In this work, we present a protocol to measure the full-dimensional coherence properties of a partially coherent beam. The method is based on tomographing the complex coherent modes of the partially coherent field within its coherence time. Once the complex coherent modes are reconstructed, all coherence properties including field correlation and its higher-order correlations (e.g., intensity correlation) can be recovered for beams that are either spatially uniformly or non-uniformly correlated. We perform a proof-of-principle experiment to measure the complex field correlation and intensity correlation of a structured partially coherent beam synthesized by random modes. Additionally, we discuss the application of full-dimensional complex coherence function tomography in coherence-based multi-cipher information security. The robustness of our system in complex environments is also evaluated. -
-
References
[1] Rubinsztein-Dunlop H, Forbes A, Berry MV et al. Roadmap on structured light. J Opt 19, 013001 (2017). doi: 10.1088/2040-8978/19/1/013001 [2] Forbes A, de Oliveira M, Dennis MR. Structured light. Nat Photonics 15, 253–262 (2021). doi: 10.1038/s41566-021-00780-4 [3] Shen YJ, Zhan QW, Wright LG et al. Roadmap on spatiotemporal light fields. J Opt 25, 093001 (2023). doi: 10.1088/2040-8986/ace4dc [4] Mandel L, Wolf E. Optical Coherence and Quantum Optics (Cambridge University Press, Cambridge, 1995). [5] Friberg AT, Setälä T. Electromagnetic theory of optical coherence [invited]. J Opt Soc Am A 33, 2431–2442 (2016). doi: 10.1364/JOSAA.33.002431 [6] Cai YJ, Chen YH, Wang F. Generation and propagation of partially coherent beams with nonconventional correlation functions: a review [invited]. J Opt Soc Am A 31, 2083–2096 (2014). [7] Yu JY, Zhu XL, Wang F et al. Research progress on manipulating spatial coherence structure of light beam and its applications. Prog Quantum Electron 91, 100486 (2023). [8] Batarseh M, Sukhov S, Shen Z et al. Passive sensing around the corner using spatial coherence. Nat Commun 9, 3629 (2018). doi: 10.1038/s41467-018-05985-w [9] Peng YF, Choi S, Kim J et al. Speckle-free holography with partially coherent light sources and camera-in-the-loop calibration. Sci Adv 7, 5040 (2021). doi: 10.1126/sciadv.abg5040 [10] Zhu L, Soldevila F, Moretti C et al. Large field-of-view non-invasive imaging through scattering layers using fluctuating random illumination. Nat Commun 13, 1447 (2022). doi: 10.1038/s41467-022-29166-y [11] Dong BW, Brückerhoff-Plückelmann F, Meyer L et al. Partial coherence enhances parallelized photonic computing. Nature 632, 55–62 (2024). doi: 10.1038/s41586-024-07590-y [12] Chen YH, Norrman A, Ponomarenko SA et al. Optical coherence and electromagnetic surface waves. Prog Opt 65, 105–172 (2020). [13] Jin Y, Wang HY, Liu L et al. Orientation-selective sub-Rayleigh imaging with spatial coherence lattices. Opt Express 30, 9548–9561 (2022). doi: 10.1364/OE.454782 [14] Liu YL, Chen YH, Wang F et al. Robust far-field imaging by spatial coherence engineering. Opto-Electron Adv 4, 210027 (2021). doi: 10.29026/oea.2021.210027 [15] Liu YL, Zhang X, Dong Z et al. Robust far-field optical image transmission with structured random light beams. Phys Rev Appl 17, 024043 (2022). doi: 10.1103/PhysRevApplied.17.024043 [16] Yu JY, Xu Y, Lin SQ et al. Longitudinal optical trapping and manipulating Rayleigh particles by spatial nonuniform coherence engineering. Phys Rev A 106, 033511 (2022). doi: 10.1103/PhysRevA.106.033511 [17] Chen YH, Wang F, Cai YJ. Partially coherent light beam shaping via complex spatial coherence structure engineering. Adv Phys: X 7, 2009742 (2022). [18] Lin R, Chen MY, Liu YL et al. Measuring refractive indices of a uniaxial crystal by structured light with non-uniform correlation. Opt Lett 46, 2268–2271 (2021). doi: 10.1364/OL.424259 [19] Li WH, Wu D, Chen YH et al. Sensing azimuthally symmetric objects by a single-pixel detector via COAM matrix. Appl Phys Lett 122, 251106 (2023). doi: 10.1063/5.0153689 [20] Zhao XC, Wang ZY, Lu XL et al. Ultrahigh precision angular velocity measurement using frequency shift of partially coherent beams. Laser Photonics Rev 17, 2300318 (2023). doi: 10.1002/lpor.202300318 [21] Lu XY, Wang ZY, Zhan QW et al. Coherence entropy during propagation through complex media. Adv Photonics 6, 046002 (2024). [22] Peng DM, Huang ZF, Liu YL et al. Optical coherence encryption with structured random light. PhotoniX 2, 6 (2021). doi: 10.1186/s43074-021-00027-z [23] Liu YL, Dong Z, Zhu YM et al. Three-channel robust optical encryption via engineering coherence Stokes vector of partially coherent light. PhotoniX 5, 8 (2024). doi: 10.1186/s43074-024-00126-7 [24] Turunen J, Halder A, Koivurova M et al. Measurement of spatial coherence of light [invited]. J Opt Soc Am A 39, C214–C239 (2022). doi: 10.1364/JOSAA.475374 [25] Arimoto H, Ohtsuka Y. Measurements of the complex degree of spectral coherence by use of a wave-front-folded interferometer. Opt Lett 22, 958–960 (1997). doi: 10.1364/OL.22.000958 [26] Santarsiero M, Borghi R. Measuring spatial coherence by using a reversed-wavefront young interferometer. Opt Lett 31, 861–863 (2006). doi: 10.1364/OL.31.000861 [27] Naraghi RR, Gemar H, Batarseh M et al. Wide-field interferometric measurement of a nonstationary complex coherence function. Opt Lett 42, 4929–4932 (2017). doi: 10.1364/OL.42.004929 [28] Takeda M, Wang W, Naik DN et al. Spatial statistical optics and spatial correlation holography: a review. Opt Rev 21, 849–861 (2014). doi: 10.1007/s10043-014-0138-2 [29] Wood JK, Sharma KA, Cho S et al. Using shadows to measure spatial coherence. Opt Lett 39, 4927–4930 (2014). doi: 10.1364/OL.39.004927 [30] Sharma KA, Brown TG, Alonso MA. Phase-space approach to lensless measurements of optical field correlations. Opt Express 24, 16099–16110 (2016). doi: 10.1364/OE.24.016099 [31] Sharma KA, Costello G, Vélez-Juárez E et al. Measuring vector field correlations using diffraction. Opt Express 26, 8301–8313 (2018). doi: 10.1364/OE.26.008301 [32] Liu X, Chen Q, Zeng J et al. Measurement of optical coherence structures of random optical fields using generalized Arago spot experiment. Opto-Electron Sci 2, 220024 (2023). doi: 10.29026/oes.2023.220024 [33] Huang ZF, Chen YH, Wang F et al. Measuring complex degree of coherence of random light fields with generalized Hanbury Brown–Twiss experiment. Phys Rev Appl 13, 044042 (2020). doi: 10.1103/PhysRevApplied.13.044042 [34] Yoneda N, Quan XY, Matoba O. Single-shot generalized Hanbury Brown–Twiss experiments using a polarization camera for target intensity reconstruction in scattering media. Opt Lett 48, 632–635 (2023). doi: 10.1364/OL.479475 [35] Lu XY, Wang ZY, Zhao CL et al. Four-dimensional experimental characterization of partially coherent light using incoherent modal decomposition. Nanophotonics 12, 3463–3470 (2023). doi: 10.1515/nanoph-2023-0288 [36] Korotkova O, Gbur G. Unified matrix representation for spin and orbital angular momentum in partially coherent beams. Phys Rev A 103, 023529 (2021). doi: 10.1103/PhysRevA.103.023529 [37] Ostrovsky AS. Coherent-Mode Representations in Optics (SPIE, Bellingham, 2006). [38] Ponomarenko SA. Complex Gaussian representation of statistical pulses. Opt Express 19, 17086–17091 (2011). doi: 10.1364/OE.19.017086 [39] Hyde IV MW, Basu S, Voelz DG et al. Experimentally generating any desired partially coherent Schell-model source using phase-only control. J Appl Phys 118, 093102 (2015). doi: 10.1063/1.4929811 [40] Hyde MW. Stochastic complex transmittance screens for synthesizing general partially coherent sources. J Opt Soc Am A 37, 257–264 (2020). [41] Hyde MW. Simulating random optical fields: tutorial. J Opt Soc Am A 39, 2383–2397 (2022). doi: 10.1364/JOSAA.465457 [42] Gori F, Santarsiero M. Devising genuine spatial correlation functions. Opt Lett 32, 3531–3533 (2007). doi: 10.1364/OL.32.003531 [43] Gori F, Ramírez-Sánchez V, Santarsiero M et al. On genuine cross-spectral density matrices. J Opt A Pure Appl Opt 11, 085706 (2009). doi: 10.1088/1464-4258/11/8/085706 [44] Martínez-Herrero R, Mejías PM, Gori F. Genuine cross-spectral densities and pseudo-modal expansions. Opt Lett 34, 1399–1401 (2009). doi: 10.1364/OL.34.001399 [45] Martínez-Herrero R, Mejías PM. Elementary-field expansions of genuine cross-spectral density matrices. Opt Lett 34, 2303–2305 (2009). doi: 10.1364/OL.34.002303 [46] Wang F, Lv H, Chen YH et al. Three modal decompositions of Gaussian Schell-model sources: comparative analysis. Opt Express 29, 29676–29689 (2021). doi: 10.1364/OE.435767 [47] Mir M, Bhaduri B, Wang R et al. Quantitative phase imaging. Prog Opt 57, 133–217 (2012). [48] Cai YJ, Chen YH, Yu JY et al. Generation of partially coherent beams. Prog Opt 62, 157–223 (2017). [49] Wang F, Liu XL, Yuan YS et al. Experimental generation of partially coherent beams with different complex degrees of coherence. Opt Lett 38, 1814–1816 (2013). doi: 10.1364/OL.38.001814 [50] Liang CH, Wang F, Liu XL et al. Experimental generation of cosine-Gaussian-correlated Schell-model beams with rectangular symmetry. Opt Lett 39, 769–772 (2014). doi: 10.1364/OL.39.000769 [51] Goodman JW. Speckle Phenomena in Optics (Roberts & Co, Englewood, 2007). [52] Yang YQ, Forbes A, Cao LC. A review of liquid crystal spatial light modulators: devices and applications. Opto-Electron Sci 2, 230026 (2023). doi: 10.29026/oes.2023.230026 [53] Wang Z, Bovik AC, Sheikh HR et al. Image quality assessment: From error visibility to structural similarity. IEEE Trans Image Process 13, 600–612 (2004). doi: 10.1109/TIP.2003.819861 [54] Kellman P, McVeigh ER. Image reconstruction in SNR units: a general method for SNR measurement. Magn Reson Med 54, 1439–1447 (2005). doi: 10.1002/mrm.20713 [55] van Dijk T, Schouten HF, Visser TD. Coherence singularities in the field generated by partially coherent sources. Phys Rev A 79, 033805 (2009). doi: 10.1103/PhysRevA.79.033805 [56] Gbur G, Visser TD. The structure of partially coherent fields. Prog Opt 55, 285–341 (2010). [57] Simula TP, Paganin DM. Coherence simplices. New J Phys 14, 113015 (2012). doi: 10.1088/1367-2630/14/11/113015 [58] Tschernig K, Martinez-Niconoff G, Busch K et al. Topological protection of partially coherent light. Photonics Res 10, 1223–1231 (2022). doi: 10.1364/PRJ.453603 [59] Ricklin JC, Davidson FM. Atmospheric turbulence effects on a partially coherent Gaussian beam: Implications for free-space laser communication. J Opt Soc Am A 19, 1794–1802 (2002). [60] Ricklin JC, Davidson FM. Atmospheric optical communication with a Gaussian Schell beam. J Opt Soc Am A 20, 856–866 (2003). doi: 10.1364/JOSAA.20.000856 [61] Liu LX, Liu WW, Wang F et al. Spatial coherence manipulation on the disorder-engineered statistical photonic platform. Nano Lett 22, 6342–6349 (2022). doi: 10.1021/acs.nanolett.2c02115 [62] Liu LX, Liu WW, Wang F et al. Ultra-robust informational metasurfaces based on spatial coherence structures engineering. Light Sci Appl 13, 131 (2024). doi: 10.1038/s41377-024-01485-3 [63] Zhang F, Guo YH, Pu MB et al. Meta-optics empowered vector visual cryptography for high security and rapid decryption. Nat Commun 14, 1946 (2023). doi: 10.1038/s41467-023-37510-z [64] Xu X, Qiao SY, Guo YH et al. Optical information encryption based on secret sharing liquid crystal elements with spatial dislocation. Laser Photonics Rev 18, 2400168 (2024). doi: 10.1002/lpor.202400168 [65] Nan T, Zhao H, Guo JY et al. Generation of structured light beams with polarization variation along arbitrary spatial trajectories using tri-layer metasurfaces. Opto-Electron Sci 3, 230052 (2024). doi: 10.29026/oes.2024.230052 -
Supplementary Information
Supplementary information for Full-dimensional complex coherence properties tomography for multi-cipher information security 
-
Access History
Article Metrics
-
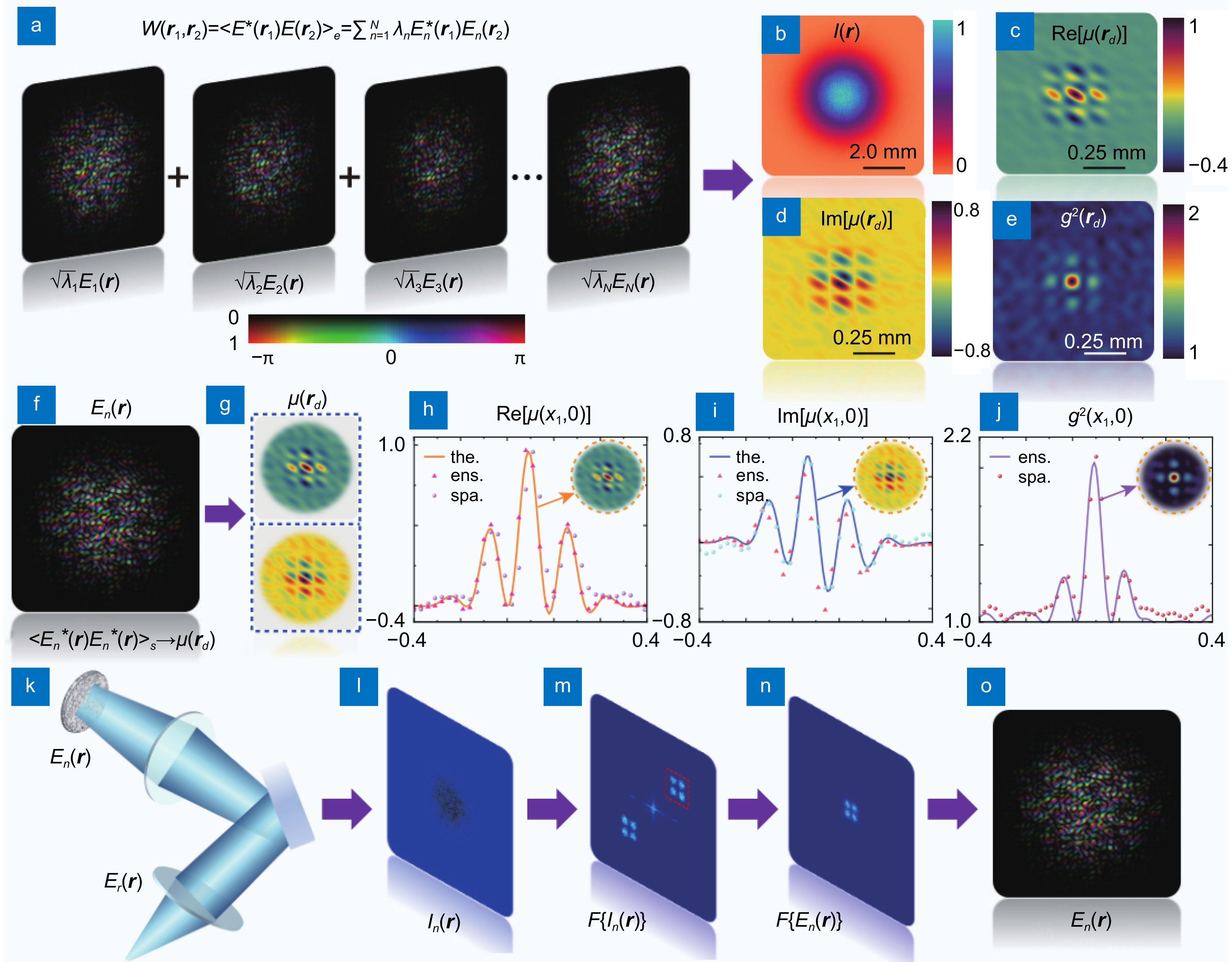
Figure 1.
(a) Random-mode representation for the CGSM beam, in which its CSD function can be decomposed as Eq. (2). The average spectral density I(r) (b), the real (c) and imaginary (d) parts of the DOC µ(rd), as well as the normalized intensity correlation g2(rd), where the reference point set as rf = 0, (e) obtained from the ensemble average over the random modes. (f) The complex field of a random mode. (g) Real and imaginary parts of the DOC extracted from the spatial correlation within the single random mode shown in (f). Cross-lines of the real part (h) and imaginary part (i) of the DOC µ(x1, 0), as well as the intensity correlation g2(x1,0) (j). The solid curves, triangle dots, and circular dots represent the results obtained from theoretical model, by the ensemble average over random modes set, and the spatial correlation within a single mode. (k–o) Schematic diagram for the retrieval of complex field of a random mode using the off-axis holography method. The beam parameters used in the calculation are ω0 = 1.0 mm, δ0 = 0.12 mm, and m = 1. The number of the random modes N used in the simulation is N = 2000.
-
Figure 2.
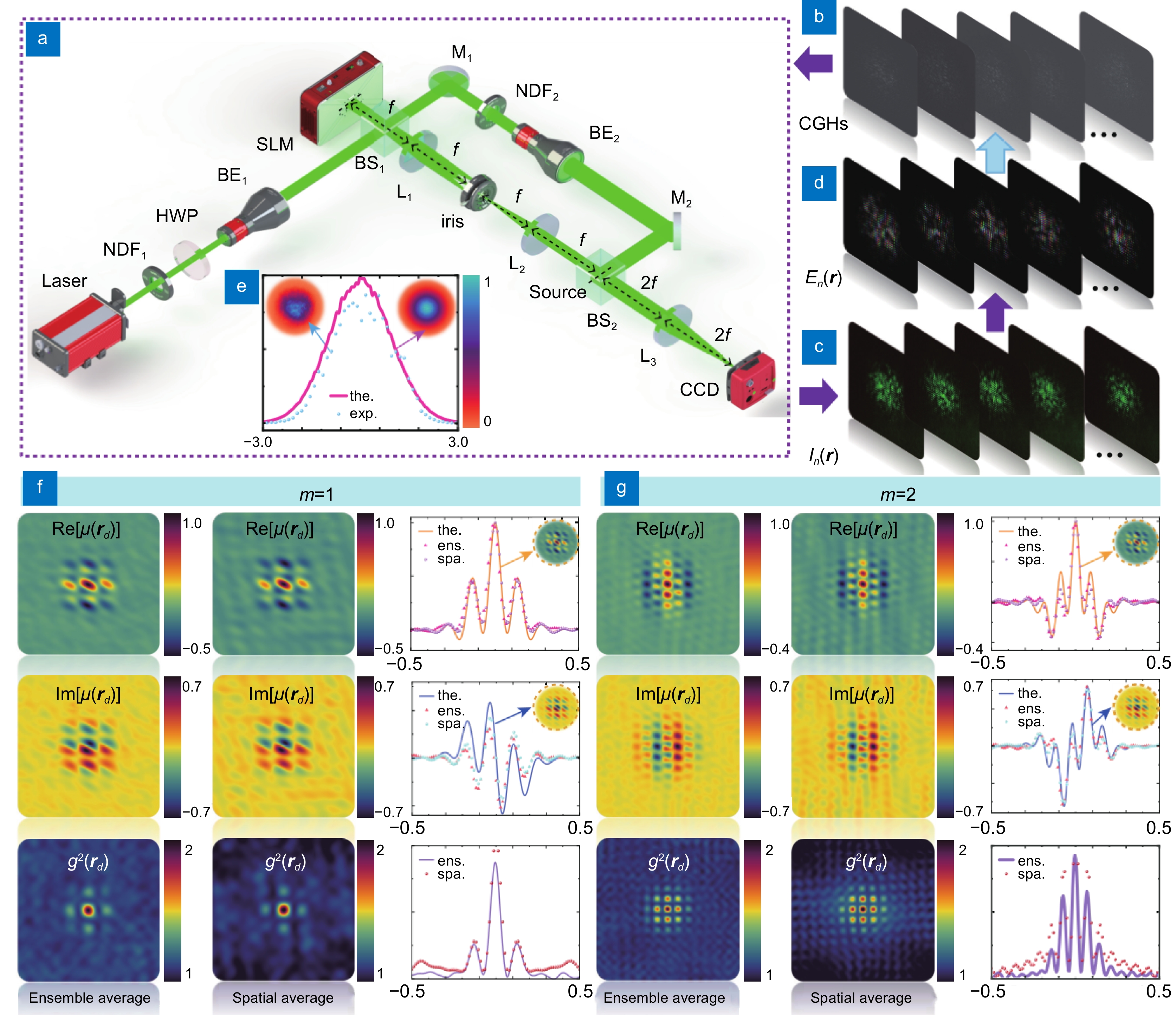
(a) Experimental setup for generating a structured partially coherent beam and measuring its mode set. (b) A series of computational generated holograms (CGHs) loaded on the SLM. (c) Instantaneous intensities of the mixed fields captured by the CCD. (d) Experimentally reconstructed complex fields of the random modes. (e) Average spectral density of the generated CGSM beam by making ensemble average over N = 2000 random modes (circular dots for cross line and density plot at the top left corner) and the corresponding theoretical result (solid curve and density plot at the top right corner). (f) The first column shows the recovered DOC and intensity correlation from the ensemble average over N = 2000 random modes. The second column shows the results obtained by the spatial correlation within a single random mode. The third column are the corresponding results for the cross lines at y1 = 0. The generated CGSM beam with m = 1. (g) The recovered DOC and intensity correlation for the CGSM beam with m = 2.
-
Figure 3.
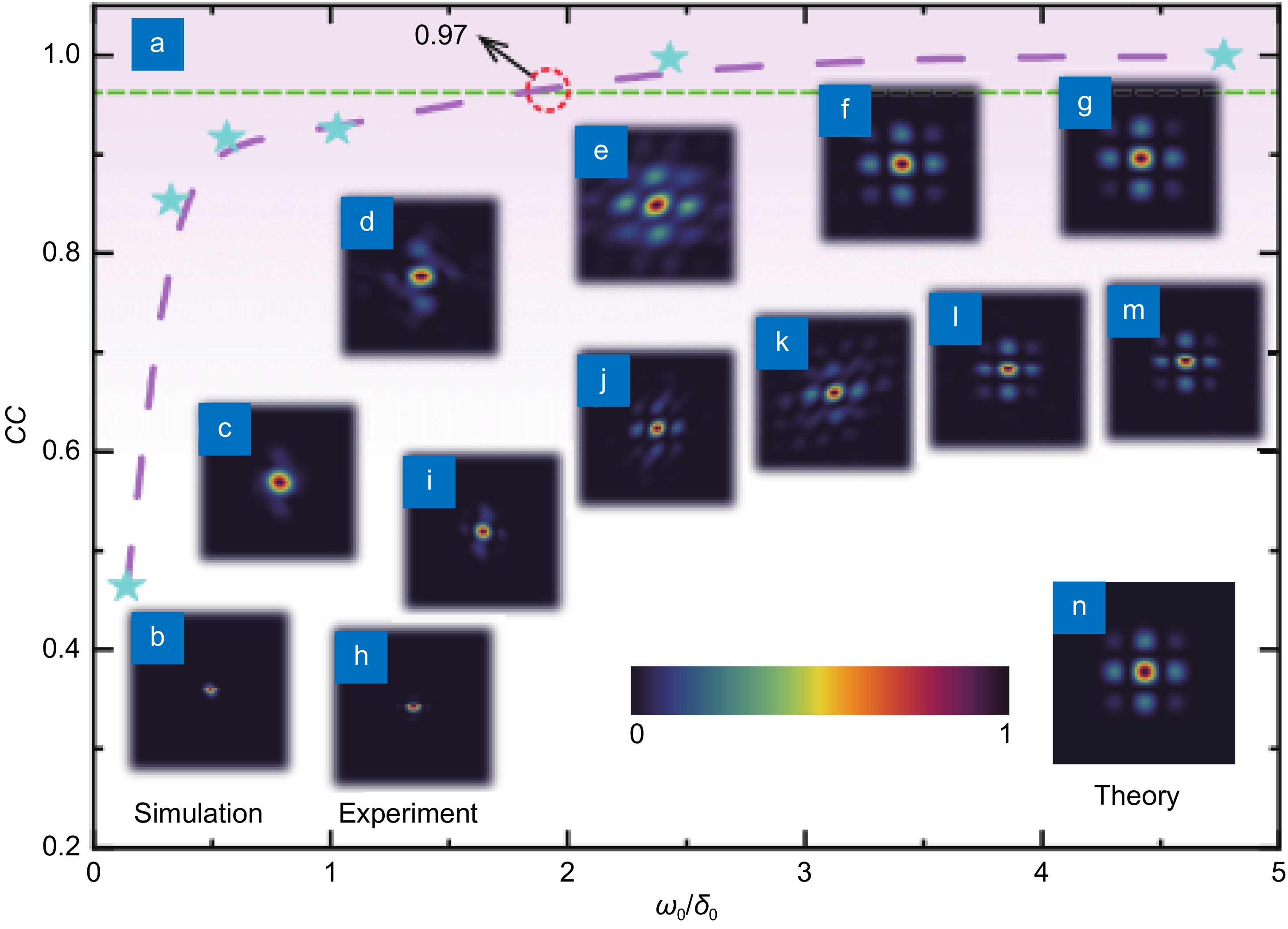
(a) The dependence of the correlation coefficient (the pentagrams for experimental results and the dashed line for simulation results) on ω0/δ0. (b–g) The modulus of the DOCs recovered from numerical simulation for different values of ω0/δ0 that correspond to those of six pentagrams. (h–m) The experimental results of the modulus of the recovered DOCs corresponding to the simulation results in (b–g). (n) The modulus of the DOC calculated from the theoretical model in Eq. (4).
-
Figure 4.
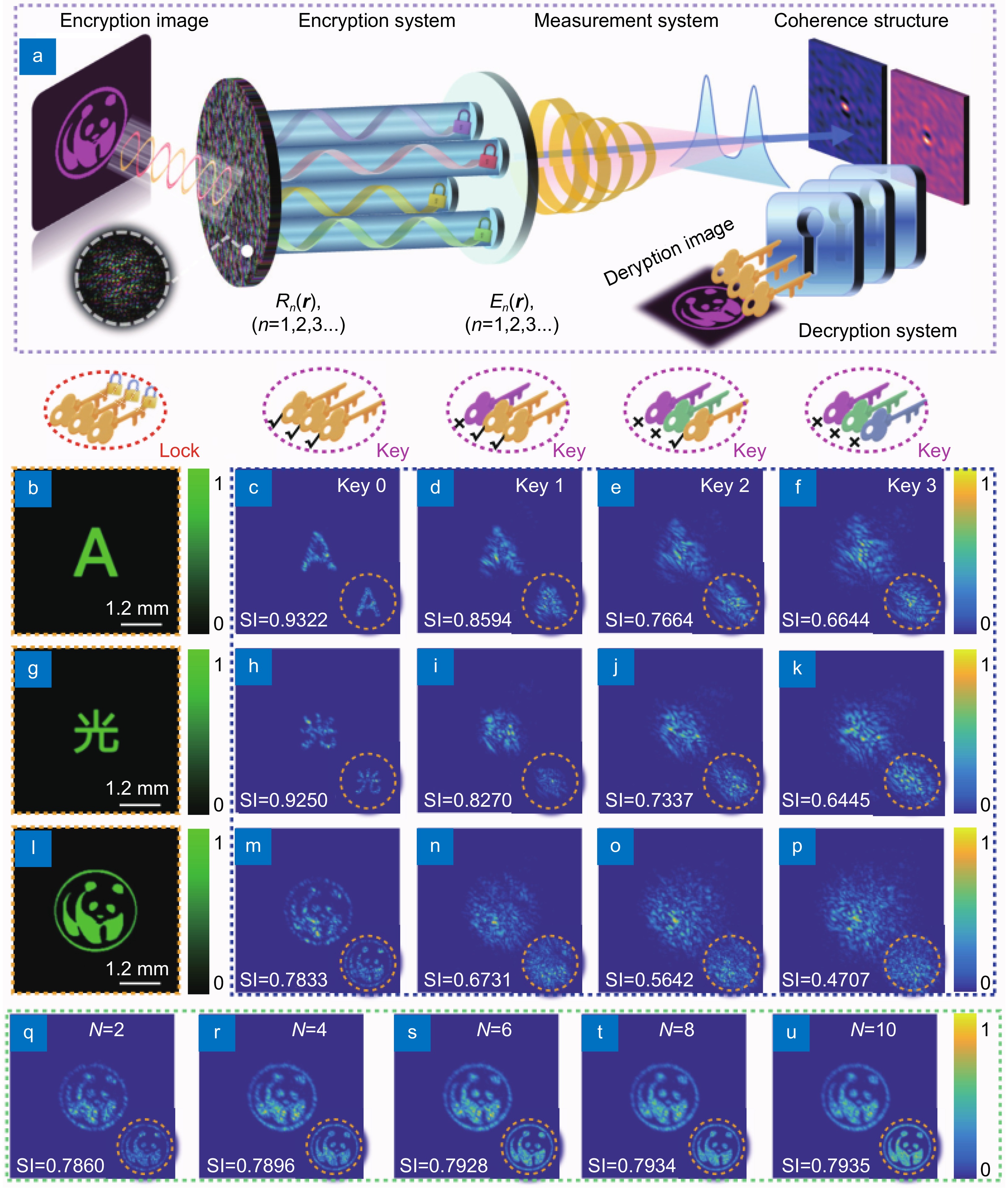
(a) Principal diagram of coherence-based multiple cipher optical image encryption and decryption. (b, g and l) are the three original images, English letter "A", Chinese character "GUANG", and the picture panda, respectively. (c–f, h–k, m–p) The decryption results for the "A", Chinese character "GUANG", and the picture panda, with different decryption keys. (q–u) Experimental results of the recovered images with different numbers N of the random modes. The corresponding simulation results for the decryption images are shown in the insets (within the yellow dashed circle).
-
Figure 5.
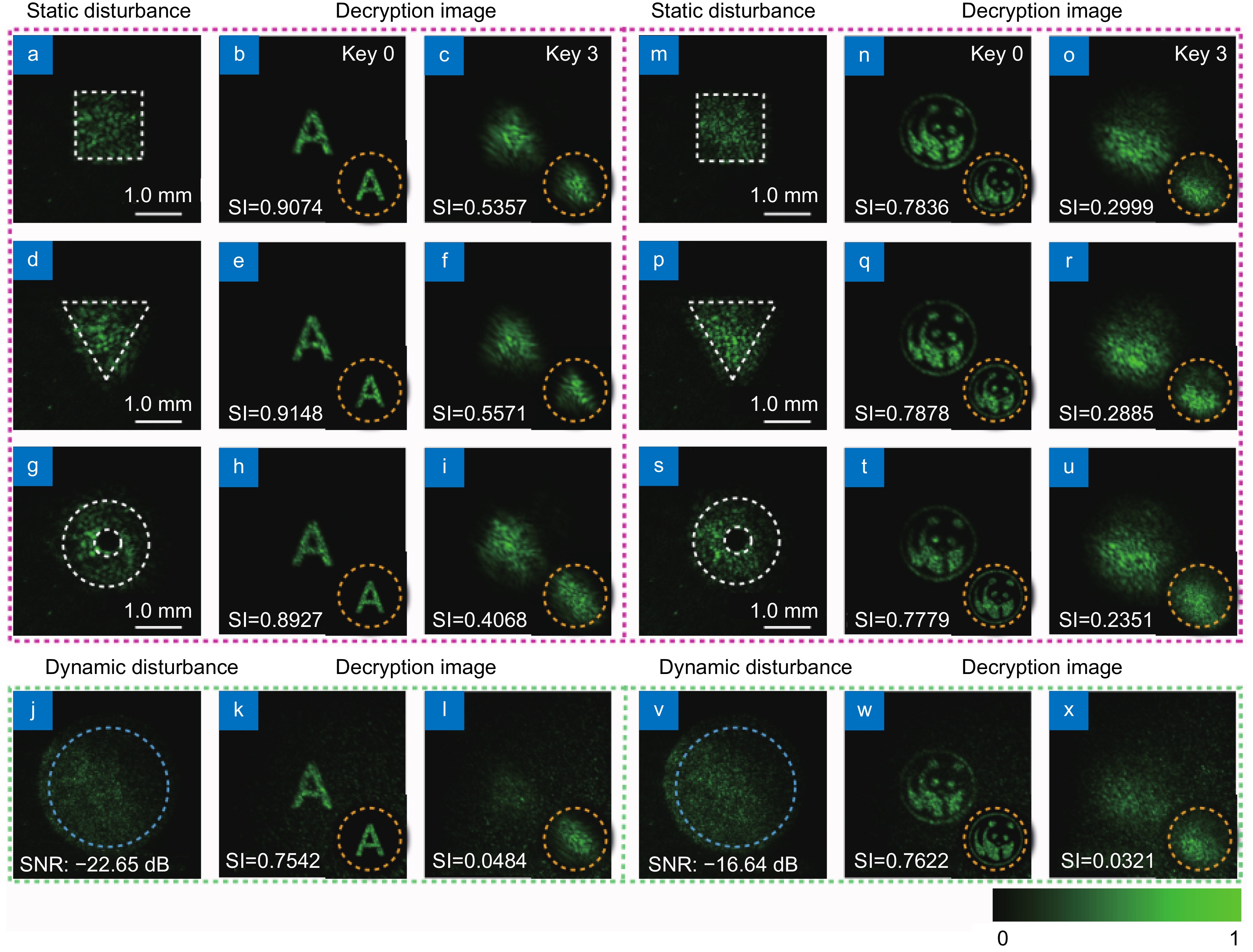
The measured speckles for a random mode when the partially coherent beam source is partially blocked by the obstacle with rectangular (a), triangular (d), and circular ring (g) openings and is disturbed by a dynamic random noise (j). (b, e, h, k) The recovered images with correct keys. (c, f, i, l) The recovered images with incorrect keys. In (a–l), the encoded image is an English letter "A". (m–x) show the corresponding experimental results for the case when the encoded image is a "panda". The insets in the recovered images are the corresponding simulation results.

 E-mail Alert
E-mail Alert RSS
RSS


 DownLoad:
DownLoad: