| Citation: | Wen Kunhua, Hu Yihua, Chen Li, et al. Subwavelength filter and sensor design based on end-coupled composited ring-groove resonator[J]. Opto-Electronic Engineering, 2017, 44(2): 192-197. doi: 10.3969/j.issn.1003-501X.2017.02.007 |
Subwavelength filter and sensor design based on end-coupled composited ring-groove resonator
-
Abstract
A plasmonic filter and sensor is designed based on an end-coupled ring-groove composited resonator (RGCR). According to the magnetic field distributions of the resonance modes, a horizontal or vertical groove is added to the perfect ring resonator, and the transmission peaks for the 1st and the 2nd modes can be linearly changed by the length of the groove. In this case, the proposed structure can act as an on-chip optical filter with flexible wavelength manipulation. When the groove is rotated with an angle of π/4, Fano resonance arises due to the mode interference. Dual asymmetric sharp transmission peaks are achieved around the wavelength of the former 2nd resonance mode. High figure of merit and high sensitivity are obtained for the structure, and it is believed that the device can find widely applications in the biochemistry sensing area. The corresponding spectra and the propagation characteristics are numerically investigated by using the finite-difference time-domain method.
-
Keywords:
- plasmonic filter /
- sensor /
- Fano resonance
-
-
References
[1] Barnes W L, Dereux A, Ebbesen T W. Surface plasmon subwavelength optics[J]. Nature, 2003, 424(6950): 824-830. doi: 10.1038/nature01937 [2] Bozhevolnyi S I, Volkov V S, Devaux E, et al. Channel plasmon-polariton guiding by subwavelength metal grooves[J]. Physical Review Letters, 2005, 95(4): 046802. doi: 10.1103/PhysRevLett.95.046802 [3] Luo Xiangang, Yan Lianshan. Surface plasmon polaritons and its applications[J]. IEEE Photonics Journal, 2012, 4(2): 590-595. doi: 10.1109/JPHOT.2012.2189436 [4] Pu Mingbo, Li Xiong, Ma Xiaoliang, et al. Catenary optics for achromatic generation of perfect optical angular momentum[J]. Science Advance, 2015, 1(9): e1500396. [5] Wen Kunhua, Hu Yihua, Chen Li, et al. Design of an optical power and wavelength splitter based on subwavelength waveguides[J]. Journal of Lightwave Technology, 2014, 32(17): 3020-3026. doi: 10.1109/JLT.2014.2333521 [6] Zhang Zhao, Shi Fenghua, Chen Yihang. Tunable multichannel plasmonic filter based on coupling-induced mode splitting[J]. Plasmonics, 2015, 10(1): 139-144. doi: 10.1007/s11468-014-9787-z [7] Gao Hongtao, Shi Haofei, Wang Changtao, et al. Surface plasmon polariton propagation and combination in Y-shaped metallic channels[J]. Optics Express, 2005, 13(26): 10795-10800. doi: 10.1364/OPEX.13.010795 [8] Lee T W, Gray S K. Subwavelength light bending by metal slit structures[J]. Optics Express, 2005, 13(24): 9652-9659. doi: 10.1364/OPEX.13.009652 [9] Wahsheh R A, Lu Zhaolin, Abushagur M A G. Nanoplasmonic couplers and splitters[J]. Optics Express, 2009, 17(21): 19033-19040. doi: 10.1364/OE.17.019033 [10] Wen Kunhua, Yan Lianshan, Pan Wei, et al. A four-port plasmonic quasi-circulator based on metal-insulator-metal waveguides[J]. Optics Express, 2012, 20(27): 28025-28032. doi: 10.1364/OE.20.028025 [11] Bavil M A, Zhou Zhipping, Deng Qingzhong. Active unidirectional propagation of surface plasmons at subwavelength slits[J]. Optics Express, 2013, 21(14): 17066-17076. doi: 10.1364/OE.21.017066 [12] Hu Feifei, Yi Huaxiang, Zhou Zhiping. Wavelength demulti plexing structure based on arrayed plasmonic slot cavities[J]. Optics Letters, 2011, 36(8): 1500-1502. doi: 10.1364/OL.36.001500 [13] Zou Xihua, Lu Bing, Pan Wei, et al. Photonics for microwave measurements[J].Laser & Photonics Review, 2016, 10(5): 711-734. [14] Zou Xihua, Liu Xinkai, Li Wangzhe, et al. Optoelectronic oscillators (OEOs) to sensing, measurement, and detection[J]. IEEE Journal of Quantum Electronics, 2016, 52(1): 0601116. [15] Pannipitiya A, Rukhlenko I D, Premaratne M, et al. Improved transmission model for metal-dielectric-metal plasmonic waveguides with stub structure[J]. Optics Express, 2010, 18(6): 6191-6204. doi: 10.1364/OE.18.006191 [16] Tao Jin, Huang Xuguang, Lin Xianshi, et al. A narrow-band subwavelength plasmonic waveguide filter with asymmetrical multiple-teeth-shaped structure[J]. Optics Express, 2009, 17(16): 13989-13994. doi: 10.1364/OE.17.013989 [17] Han Zhanghua, Forsberg E, He Sailing. Surface plasmon bragg gratings formed in metal-insulator-metal waveguides[J]. IEEE Photonics Technology Letters, 2007, 19(2): 91-93. doi: 10.1109/LPT.2006.889036 [18] Wang Bing, Wang Guoping. Plasmon bragg reflectors and nanocavities on flat metallic surfaces[J]. Applied PhysicsLetters, 2005, 87(1): 013107. [19] Luo Xin, Zou Xihua, Li Xiaofei, et al. High-uniformity multichannel plasmonic filter using linearly lengthened insulators in metal–insulator–metal waveguide[J]. Optics Letters, 2013, 38(9): 1585-1587. doi: 10.1364/OL.38.001585 [20] Xiao Sanshui, Liu Liu, Qiu Min. Resonator channel drop filters in a plasmon-polaritons metal[J]. Optics Express, 2006, 14(7): 2932-2937. doi: 10.1364/OE.14.002932 [21] Liu Ye, Zhou Fei, Yao Bo, et al. High-extinction-ratio and low-insertion-loss Plasmonic Filter with Coherent Coupled Nano-cavity Array in a MIM Waveguide[J]. Plasmonics, 2013, 8(2):1035-1041. doi: 10.1007/s11468-013-9506-1 [22] Lu Hua, Liu Xueming, Wang Guoxi, et al. Tunable high-channel- count bandpass plasmonic filters based on an analogue of electromagnetically induced transparency[J]. Nanotechnology, 2012, 23(44): 444003. doi: 10.1088/0957-4484/23/44/444003 [23] Wu Yaw-Dong. High transmission efficiency wavelength division multiplexer based on metal–insulator–metal plasmonic waveguides[J]. Journal of Lightwave Technology, 2014, 32(24): 4242-4246. [24] Zhang Huiyun, Shen Duanlong, Zhang Yuping. Circular split-ring core resonators used in nanoscale metal–insulator–metal band-stop filters[J]. Laser Physics Letters, 2014, 11(11): 115902. doi: 10.1088/1612-2011/11/11/115902 [25] Wang Guoxi, Lu Hua, Liu Xueming, et al. Tunable multi-channel wavelength demultiplexer based on MIM plasmonic nanodisk resonators at telecommunication regime[J]. Optics Express, 2011, 19(4): 3513-3518. doi: 10.1364/OE.19.003513 [26] Lu Hua, Liu Xueming, Mao Dong, et al. Tunable band-pass plasmonic waveguide filters with nanodisk resonators[J]. Optics Express, 2010, 18(17): 17922-17927. doi: 10.1364/OE.18.017922 [27] Guo Yinghui, Yan Lianshan, Pan Wei, et al. A plasmonic splitter based on slot cavity[J]. Optics Express, 2011, 19(5): 13831-13838. [28] Fano U. Effects of configuration interaction on intensities and phase shifts[J]. Physical Review, 1961, 124(6): 1866-1878. doi: 10.1103/PhysRev.124.1866 [29] Chen Jianjun, Li Zhi, Zou Yujiao, et al. Coupled-resona tor-induced fano resonances for plasmonic sensing with ultra-high figure of merits[J]. Plasmonics, 2013, 8(4): 1627-1631. doi: 10.1007/s11468-013-9580-4 [30] Lu Hua, Liu Xueming, Mao Dong, et al. Plasmonic nanosensor based on Fano resonance in waveguide-coupled resonators[J]. Optics Letters, 2012, 37(18): 3780-3782. doi: 10.1364/OL.37.003780 [31] Wen Kunhua, Hu Yihua, Chen Li, et al. Fano resonance with ultra-high figure of merits based on plasmonic metal-insula tor-metal waveguide[J]. Plasmonics, 2015, 10(1): 27-32. doi: 10.1007/s11468-014-9772-6 [32] Wen Kunhua, Hu Yihua, Chen Li, et al. Single/dual Fano resonance based on plasmonic metal-dielectric-metal waveguide[J]. Plasmonics, 2016, 11(1): 315-321. doi: 10.1007/s11468-015-0056-6 [33] Dionne J A, Sweatlock L A, Atwater H A, et al. Plasmon slot waveguides: towards chip-scale propagation with subwave length-scale localization[J]. Physical Review B, 2006, 73(3): 035407. doi: 10.1103/PhysRevB.73.035407 [34] Johnson P B, Christy R W. Optical constants of the noble metals[J]. Physical Review B, 1972, 6(12): 4370-4379. doi: 10.1103/PhysRevB.6.4370 [35] Becker J, Trügler A, Jakab A, et al. The optimal aspect ratio of gold nanorods for plasmonic bio-sensing[J]. Plasmonics, 2010, 5(2): 161-167. doi: 10.1007/s11468-010-9130-2 -
Overview

Abstract: Based on the metal-insulator-metal (MIM) waveguide structures, a plasmonic filter and a sensor are designed by using an end-coupled ring-groove composited resonator (RGCR). It is well known that the perfect ring (PR) cavity can be regarded as a Fabry-Pérot resonator, and the transmission wavelengths of all the resonance modes are determined by its perimeter. According to the magnetic field distributions of the 1st and the 2nd resonance modes inside the PR cavity, a groove is added in the horizontal or the normal position of the ring cavity to manipulate the wavelength of the only expected mode in this paper. Specifically, when the groove locates at the anti-node of magnetic field, SPPs will be captured into the groove, and then the resonance wavelength is changed by the groove. On the contrary, when the groove locates at the node, the corresponding SPP mode will not be affected by the groove. When the inner and outer radius are 150 and 220 nm, the 1st and the 2nd resonance wavelengths for the PR cavity are 890.6 and 1784.4 nm, respectively. To manipulate the wavelengths of the modes, the groove is firstly placed at the top of the PR, where are the anti-node and the node for the 2nd and the 1st modes, respectively. The wavelength for the 2nd mode is linearly changed by the length of the groove, while the 1st mode keeps no change. Secondly, the groove is placed in the horizontal position, where the anti-nodes for both SPPs modes emerge. Likewise, it is investigated that the center wavelengths for both modes have linearly redshifted by increasing the length of the groove. In this case, the structure can be used as an on-chip optical filter with flexible wavelength manipulation. In addition, when the groove is rotated with an angle of p/4, Fano resonance will arise due to the mode interferences. Dual asymmetric sharp transmission peaks are achieved around the wavelength of the former 2nd resonance mode, and the resonance wavelengths for both Fano peaks are also tuned by the length of the groove. High figure of merit of 4.1×104 and high refractive-index sensitivity of 970 nm/RIU are obtained for the structure. Therefore, it is believed that the device can find wide applications in the biochemistry sensing area. It is also investigated that normal and abnormal dispersions are available at the peaks and dips, respectively. The corresponding spectra and the propagation characteristics are numerically investigated by using the finite-difference time-domain method. The proposed structure can provide important support for the development of highly integrated photonics circuits and on-chip optical sensors.
-
Access History
Article Metrics
-
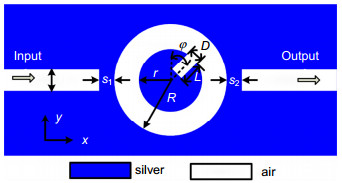
Figure 1.
Schematic diagram of the proposed plasmonic RGCR structure.
-
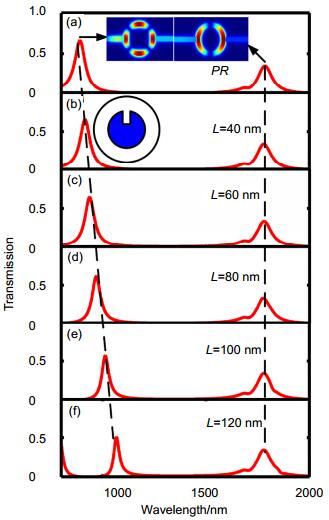
Figure 2.
Transmission spectra of (a) PR resonator, and (b)~(f) RGCR structures with φ=0°, and L=40, 60, 80, 100, and 120 nm, respectively.
-
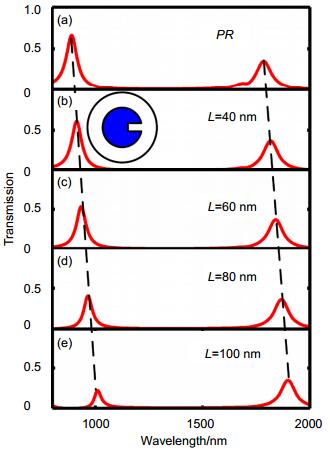
Figure 3.
Transmission spectra of (a) perfect ring resonator, (b)~(f) PR structure with φ=90°, and L=40, 60, 80, and 100 nm, respectively.
-
Figure 4.
(a) Transmission spectra of PR resonator and RGCR structure with φ=90° and L=100 nm, and (b) phase response and delay time.
-
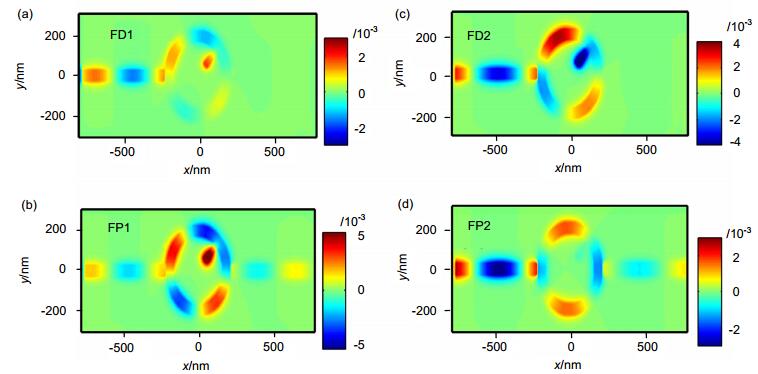
Figure 5.
Magnetic field distribution at the wavelengths of (a) FD1, (b) FP1, (c) FD2 and (d) FP2.
-
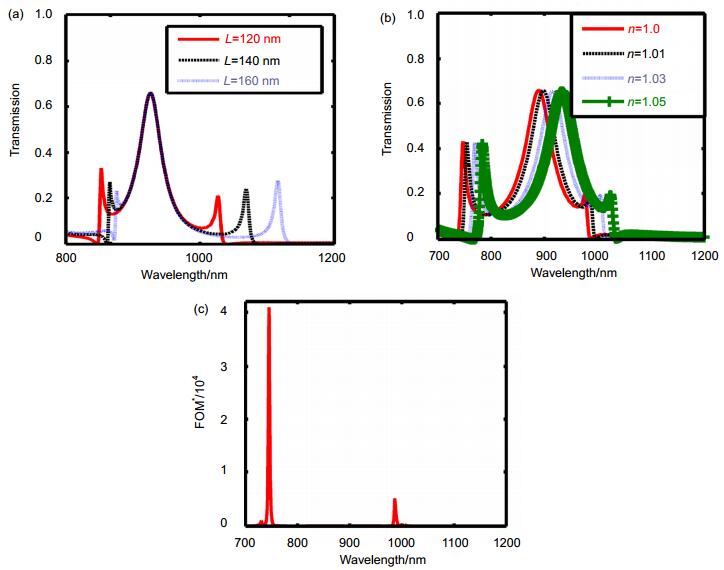
Figure 6.
(a) Fano resonance spectra with L=120, 140 and 160 nm. (b) Fano resonance spectra with L=100 nm and n=1.0, 1.01, 1.03 and 1.05. (c) FOM* variation with respect to wavelength.

 E-mail Alert
E-mail Alert RSS
RSS


 DownLoad:
DownLoad: