| Citation: | Li QY, Liang MG, Liu SQ et al. Phase reconstruction via metasurface-integrated quantum analog operation. Opto-Electron Adv 8, 240239 (2025). doi: 10.29026/oea.2025.240239 |
Phase reconstruction via metasurface-integrated quantum analog operation
-
Abstract
Phase reconstruction plays a pivotal role in biology, medical imaging, and wavefront sensing. However, multiple measurements and adjustments are usually required for conventional schemes, which inevitably reduces the quality of phase imaging. Here, based on multi-channel metasurface and quantum entanglement source, a simple and integrated quantum analog operation system is proposed to realize quantitative phase reconstruction with a high signal-to-noise ratio (SNR) under a low signal photon level. Without additional measurements and adjustments, four differential images necessary for the phase reconstruction are captured simultaneously. The non-local correlation of entangled photon pairs enables to remotely manipulate working modes of the system. Besides, the consistency of entangled photon pairs in time domain makes it possible to achieve a high SNR imaging by trigger detection. The results may potentially empower the application of metasurfaces in optical chip, wave function reconstruction, and label-free biology imaging. -
Introduction
With the unique advantages in label-free imaging and material characterization1−6, the phase reconstruction of light field provides an important scientific basis for the detection of biological samples and disease diagnosis7. Since the oscillation frequency of the optical wavefront is much higher than the response frequency of the human eye or detector, the phase of the optical wavefront is difficult to be directly detected8. With several typical branches, the combination of digital holography and optical imaging seems to solve this difficulty, including optical diffraction tomography9, holographic multiplexing10, and deep learning11. However, complex devices and multiple measurements are usually required in some schemes, which inevitably affect the imaging quality12−15. Therefore, how to integrate devices and reduce unnecessary operations remains a significant challenge to achieve accurate quantitative phase reconstruction.
The metasurface, which constitutes a compact nano-photonics platform for effective light field manipulation, is a suitable candidate to solve the above challenge16−22. By customizing tailored photonic response in metasurfaces, the amplitude, phase, and polarization of light can be accurately tuned23−29, which simplify the complex optical information processing to an optical analog operation30−37. The introduction of the optical analog operation on metasurface into the quantitative phase reconstruction provides a possible scheme for obtaining high-contrast images of transparent objects38−42. However, for some photosensitive samples, such as yeast and neuron cells, the imaging system needs to be operated under low signal light conditions43−45, while the overwhelming ambient shot noise determines that conventional imaging schemes have a low signal-to-noise ratio (SNR)46−48. Consequently, how to realize quantitative phase reconstruction with a high SNR under low signal light conditions is still a critical problem.
In this paper, based on multi-channel metasurface and quantum entanglement source, a simple and integrated quantum analog operation system is proposed to realize quantitative phase reconstruction with a high SNR under a low signal photon level. In the experiment, four differential operations are implemented simultaneously on the same metasurface, which are required for obtaining the phase gradient. Then, the quantitative reconstruction can be realized by performing Fourier integral operation and solving optimization problem for the phase gradient. Combined with the quantum entanglement source, sister photons of the imaging photon can be used as the external trigger signal of the detector to control the shutter switch, which can filter out most of the ambient noise and obtain the images with an improved SNR. Besides, the multi-channel and non-local switching of mode selection is realized through the polarization correlation of entangled photon pairs. The proposed method of phase reconstruction may pave the way for the applications of metasurfaces in optical chip, wave function reconstruction, and label-free biology imaging.
Methods
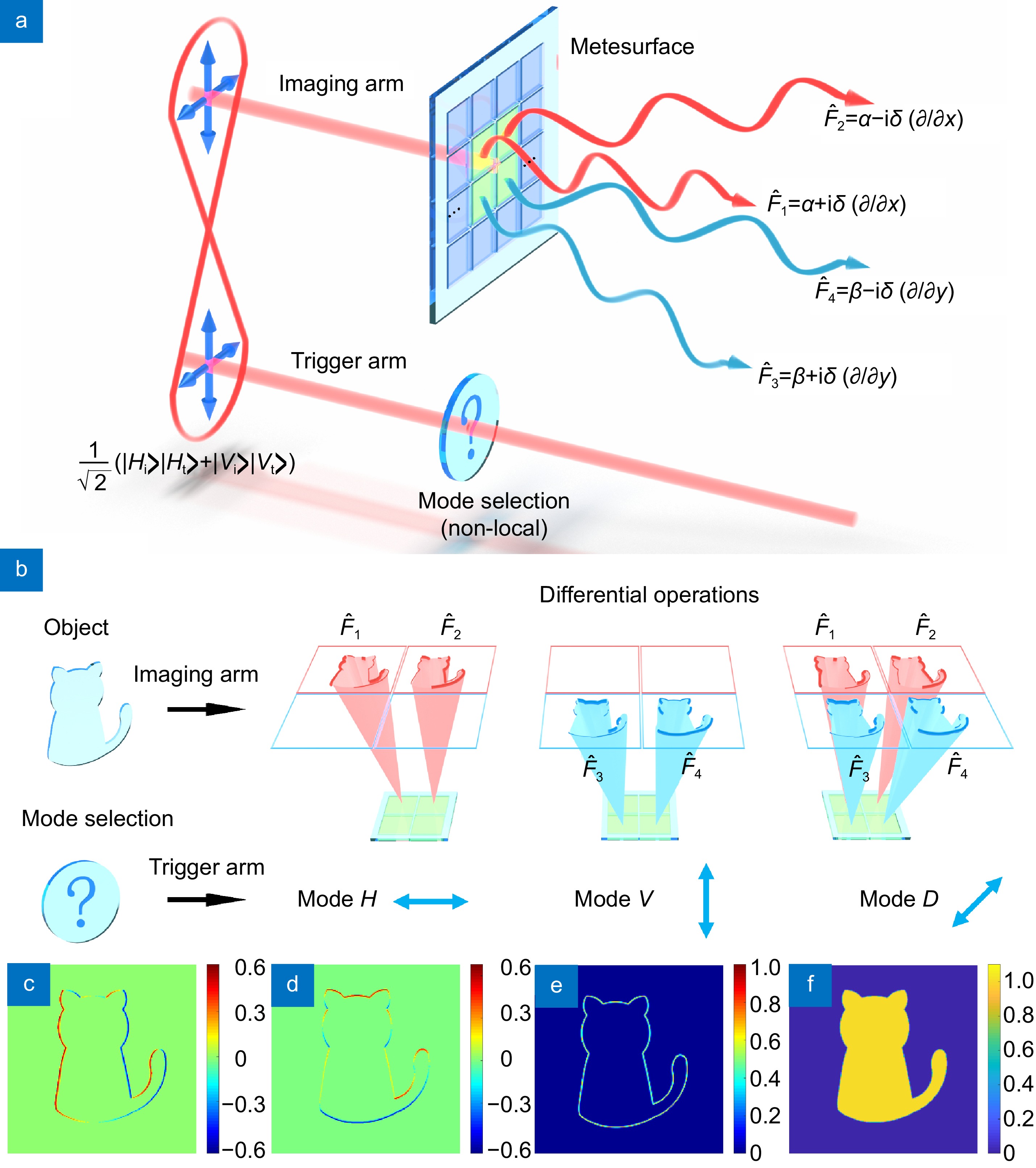
Based on a multifunctional metasurface, the concept of metasurface-integrated analog operation system is proposed, which has four polarization-dependent channels to perform different modes. On this basis, combined with the quantum entanglement source system, the remote switching of the working mode can be realized. As shown in Fig. 1(a), the entangled photon pair is in the first Bell state:
 Figure 1. Phase reconstruction via metasurface-integrated quantum analog operation. (a) Schematic of non-local mode selection by metasurface-integrated quantum analog operation. ˆF1, ˆF2, ˆF3, and ˆF4 are the differential operators. The green area has been designed to construct differential operators, and the blue area can be extended to construct other operators. (b) Three modes of metasurface-integrated quantum analog operation system and corresponding differential output results through non-local mode selection. (c) Theoretical phase gradient in x-direction. (d) Theoretical phase gradient in y-direction. (e) Theoretical two-dimensional (2D) phase gradient. (f) Theoretical phase distribution calculated by the 2D phase gradient.
Figure 1. Phase reconstruction via metasurface-integrated quantum analog operation. (a) Schematic of non-local mode selection by metasurface-integrated quantum analog operation. ˆF1, ˆF2, ˆF3, and ˆF4 are the differential operators. The green area has been designed to construct differential operators, and the blue area can be extended to construct other operators. (b) Three modes of metasurface-integrated quantum analog operation system and corresponding differential output results through non-local mode selection. (c) Theoretical phase gradient in x-direction. (d) Theoretical phase gradient in y-direction. (e) Theoretical two-dimensional (2D) phase gradient. (f) Theoretical phase distribution calculated by the 2D phase gradient.|ϕ+⟩=1√2(|Hi⟩Ht⟩+|Vi⟩|Vt⟩), (1) where the subscripts i and t represent imaging photon and trigger photon, used to extract the sample information and control the detector switch, respectively. |H⟩ and |V⟩ are horizontal and vertical polarization states. Equation (1) indicates that when the polarization state of trigger photon is set as |Ht⟩ (|Vt⟩), the imaging photon will be collapsed to |Ht⟩ (|Vt⟩) simultaneously. The optical axes of the four working regions on the metasurface all change periodically in one dimensional (1D) direction with the spatial period of Λ. After passing through arbitrary working region of the metasurface, the imaging photon will produce a spin-dependent shift δ=−σ±(λz/Λ), where σ=±1 indicate the left-circularly polarized (LCP) and right-circularly polarized light (RCP), respectively, and z is the transmission distance of the imaging photon49.
Assuming that the imaging photon may pass through the center of four regions, four differential operators ˆF1=(α+iδ(∂/∂x)), ˆF2=(α−iδ(∂/∂x)), ˆF3=(β+iδ(∂/∂y)), and ˆF4=(β−iδ(∂/∂y)) can be constructed. Here, α and β are the tiny angles which the optical axes deviating from the H- and V-directions, respectively. The initial spatial wave function of the imaging photon can be expressed as |Ψsp⟩in. After being affected by ˆFi(i=1,2,3,4), the wave function will evolve to |Ψsp⟩out=ˆFi|Ψsp⟩in. Eventually, the intensity distribution of photons on the detector can be given as (see Section 1 in the Supplementary information):
P(1)out(x,y)=⟨Ψsp|Ψsp⟩(1)out≈cos2γPin(x,y)⋅{α2+[δ∂φ(x,y)∂x]2−2αδ∂φ(x,y)∂x},P(2)out(x,y)=⟨Ψsp|Ψsp⟩(2)out≈cos2γPin(x,y)⋅{α2+[δ∂φ(x,y)∂x]2+2αδ∂φ(x,y)∂x},P(3)out(x,y)=⟨Ψsp|Ψsp⟩(3)out≈sin2γPin(x,y)⋅{β2+[δ∂φ(x,y)∂x]2−2βδ∂φ(x,y)∂x},P(4)out(x,y)=⟨Ψsp|Ψsp⟩(4)out≈sin2γPin(x,y)⋅{β2+[δ∂φ(x,y)∂x]2+2βδ∂φ(x,y)∂x}, (2) where γ is the polarization angle, and Pin(x,y)=⟨Ψsp|Ψsp⟩ represents the initial intensity distribution. Notably, the four-channel metasurface helps to simultaneously capture the four results shown in Eq. (2), which are necessary to achieve phase reconstruction based on differential operations. In conventional schemes, multiple adjustments of the optical path are involved to capture the above results, inevitably increasing complexity and decreasing accuracy. After linearly combining the above Eq. (2), quantitative phase gradient can be obtained by
\nabla \varphi (x,y) = \frac{{{\mathrm{\Delta}} P_{{\mathrm{out}}}^x(x,y)}}{{2\alpha \delta {{\cos }^2}\gamma {P_{{\mathrm{in}}}}(x,y)}}{ {\boldsymbol{e}} _x} + \frac{{{\mathrm{\Delta}} P_{{\mathrm{out}}}^y(x,y)}}{{2\beta \delta {{\sin }^2}\gamma {P_{{\mathrm{in}}}}(x,y)}}{ {\boldsymbol{e}} _y}\;, (3) where {\mathrm{\Delta}} P_{{\mathrm{out}}}^x and {\mathrm{\Delta}} P_{{\mathrm{out}}}^y can be expressed as
\begin{gathered} {\mathrm{\Delta}} P_{{\mathrm{out}}}^x(x,y) = P_{{\mathrm{out}}}^{(2)}(x,y) - P_{{\mathrm{out}}}^{(1)}(x,y)\;, \\ {\mathrm{\Delta}} P_{{\mathrm{out}}}^y(x,y) = P_{{\mathrm{out}}}^{(4)}(x,y) - P_{{\mathrm{out}}}^{(3)}(x,y)\;. \\ \end{gathered} (4) Specially, since the imaging and the trigger photons have polarization entanglement, when the trigger photon is polarized at \gamma = {0^\circ},{90^\circ},{45^\circ} , the imaging photon will collapse into the same polarization state simultaneously. Under this basic principle, the non-local control of the differential operator can be achieved [Fig. 1(b)]. In particular, the quantum analog operation system can still function properly when the light source does not match the designed working wavelength50 (see Section 2 in the Supplementary information).
Considering the case in which the light is emitted to phase objects, such as transparent biological cells50−53, the amplitude of the input light field is hardly affected due to the weak absorption feature of light, and only phase information \varphi (x,y) of the object will be introduced. Therefore, after the imaging photon passes through the phase object, the spatial wave function can be expressed as \left| {{\Psi _{{\mathrm{sp}}}}(x,y)} \right\rangle = {\mathrm{exp}} [{\mathrm{i}}\varphi (x,y)]\left| {\psi (x,y)} \right\rangle , where \left| {\psi (x,y)} \right\rangle represents the initial wave function of the imaging photon. If the polarization state of trigger photon is set as \left| D \right\rangle , the wave function input to the metasurface can be expressed as
|{\Psi _{{\mathrm{tol}}}}(x,y){\rangle _{{\mathrm{in}}}} = \psi (x,y){\mathrm{exp}} [{\mathrm{i}}\varphi (x,y)]|D\rangle \;. (5) Subsequently, according to the Fourier integral theorem, normalized phase distribution can be calculated as45
\phi (x,y) = {\mathcal{F}^{ - 1}}\left\{ {\mathcal{F}\left[ {\frac{{\partial \varphi (x,y)}}{{\partial x}} + {\mathrm{i}}\frac{{\partial \varphi (x,y)}}{{\partial y}}} \right]/({\mathrm{i}}{k_x} - {k_y})} \right\}, (6) where \mathcal{F} and {\mathcal{F}^{ - 1}} represent the Fourier and inverse Fourier transforms, {k_x} and {k_y} represent wave vectors in the x- and y-directions, respectively. However, compared with the true phase distribution \varphi (x,y), the normalized reconstructed phase distribution \phi (x,y) differs by a normalized factor K, which is necessary for quantitative phase reconstruction. Since differential operations are linear operations, the following relation holds:
\frac{{\varphi (x,y)}}{{\phi (x,y)}} = \frac{{\nabla \varphi (x,y)}}{{\nabla \phi (x,y)}}\;, (7) where \nabla \phi (x,y) is calculated numerically by \phi (x,y). According to Eq. (7), the residual difference, which is between the measured phase gradient \nabla \varphi (x,y) and the reconstructed phase gradient K\nabla \phi (x,y), can be defined as
S(K) = \sum\limits_{{\mathrm{Pixel}}} | \nabla \varphi (x,y) - K\nabla \phi (x,y)|\;. (8) By calculating the minimum value of the residual difference S(K), the optimal normalization coefficient K is obtained. Consequently, quantitative phase reconstruction results can be described as
\varphi (x,y) = K\phi (x,y). (9) Results and discussion
Quantum analog operation enables non-local mode selections
The experimental setup of metasurface-integrated quantum analog operation system is presented in Fig. 2, and the polarization entanglement source of \beta\text{-}{\mathrm{Ba}}{{\mathrm{B}}_2}{{\mathrm{O}}_4} crystals (BBOs)51,52 is the key to achieve the non-local mode selection with a high SNR. In order to improve the quality of the polarization entanglement source, a polarization beam splitter (PBS), a half-wave plate (HWP) and a quarter-wave plate (QWP) are used to calibrate the polarization state of the pump beam. Moreover, the quartz crystal (QC) is used to compensate the phase difference between the H- and V- components. The optical path associated with the object is considered as the imaging arm, while the other path used for remote mode selection is the trigger arm. Notably, there is a non-local correlation exists between the imaging photon and the trigger photon. The polarization entanglement is the key to realizing remote control, which only requires the P1 to set the polarization state of trigger photon to \left| \gamma \right\rangle . As a result, the polarization state of the imaging photon will be directly collapse to the same polarization state \left| \gamma \right\rangle without any operation in imaging arm. The inset of Fig. 2 shows the polarization interference curves at H/V and D/A bases which demonstrates that the BBO quantum entanglement source meets the requirement of quantum analog operation53,54 (see Section 3 in the Supplementary information). Here, |D\rangle = (1/\sqrt 2 )\left( {|H\rangle + |V\rangle } \right) and |A\rangle = (1/\sqrt 2 )\left( {|H\rangle - |V\rangle } \right) denote the linearly polarized states with polarization angles of 45^\circ and - 45^\circ , respectively.
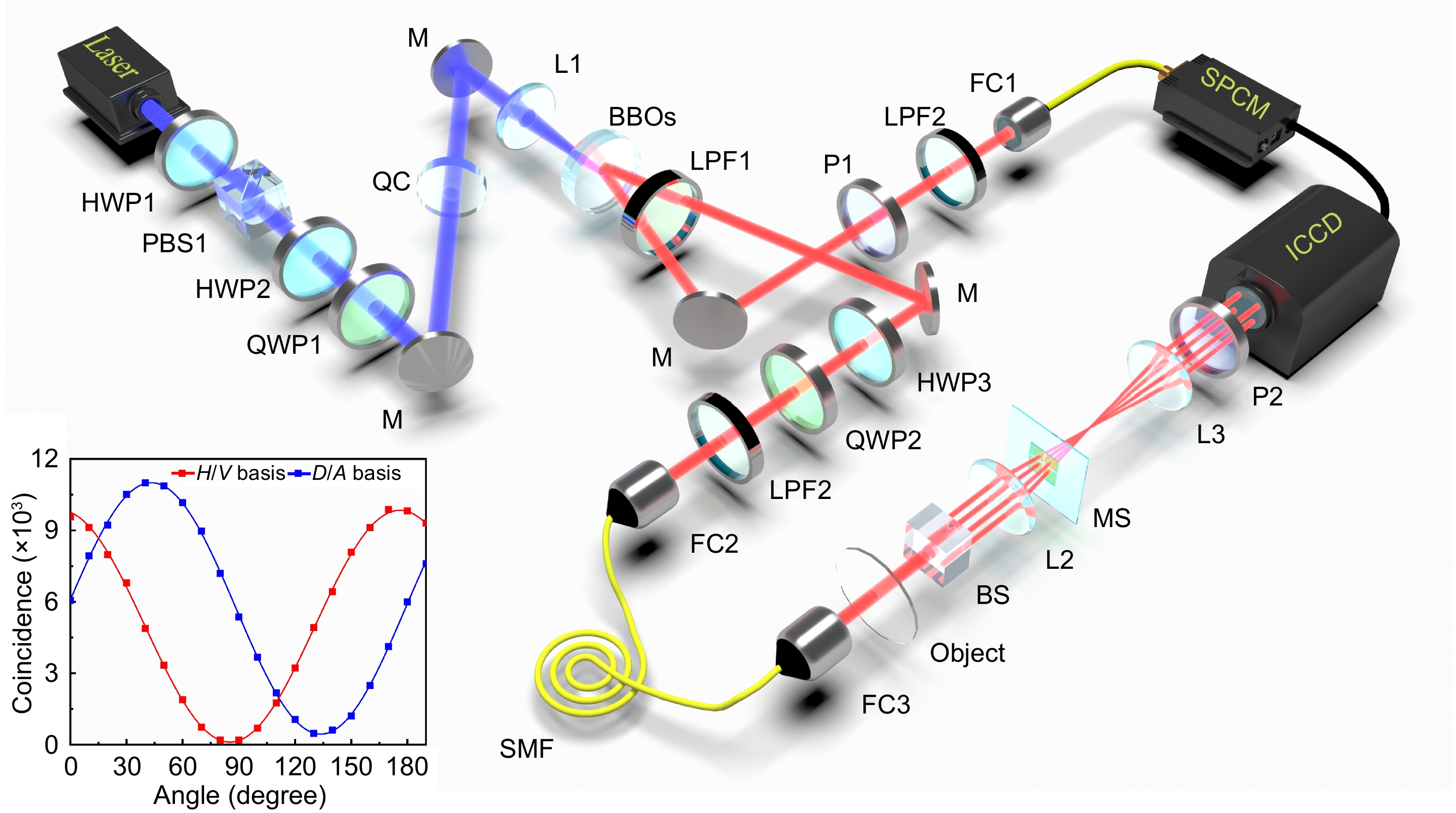 Figure 2. Experimental setup. Setup schematic: HWP, half-wave plate; QWP, quarter-wave plate; PBS, polarization beam splitter; M, mirror; QC, quartz crystal; L, Lens; BBOs, β-BaB2O4 crystals; LPF, long-pass filter; FC, fiber coupler; BS, beam splitter; SMF, single mode fiber; SPCM, single photon counting module; ICCD, intensified charge coupled device. Inset, the experimental results of the polarization interference curves.
Figure 2. Experimental setup. Setup schematic: HWP, half-wave plate; QWP, quarter-wave plate; PBS, polarization beam splitter; M, mirror; QC, quartz crystal; L, Lens; BBOs, β-BaB2O4 crystals; LPF, long-pass filter; FC, fiber coupler; BS, beam splitter; SMF, single mode fiber; SPCM, single photon counting module; ICCD, intensified charge coupled device. Inset, the experimental results of the polarization interference curves.Integrated metasurface generates four differential operations simultaneously
As shown in Fig. 2, the beam will be divided into four parts by beam splitter (BS) system according to polarization (see Section 4 in the Supplementary information), where \left| H \right\rangle and \left| V \right\rangle photons are sent to the upper and lower channels, respectively. In the 4f system, lens L2 and lens L3 play the role of focusing and restoring Gaussian wavefront respectively. The photons in each output channel of BS pass through different regions on the metasurface (see Section 5 in the Supplementary information), producing different spin-dependent shifts. As shown in Fig. 3(e), the four channels of the metasurface have periodically varying optical axes and a uniform birefringent phase delay \pi . As a result, the polarization state of each photon passing through the metasurface will be inverted and the conversion efficiency is experimentally demonstrated to be greater than 96% (see Section 6 in the Supplementary information).
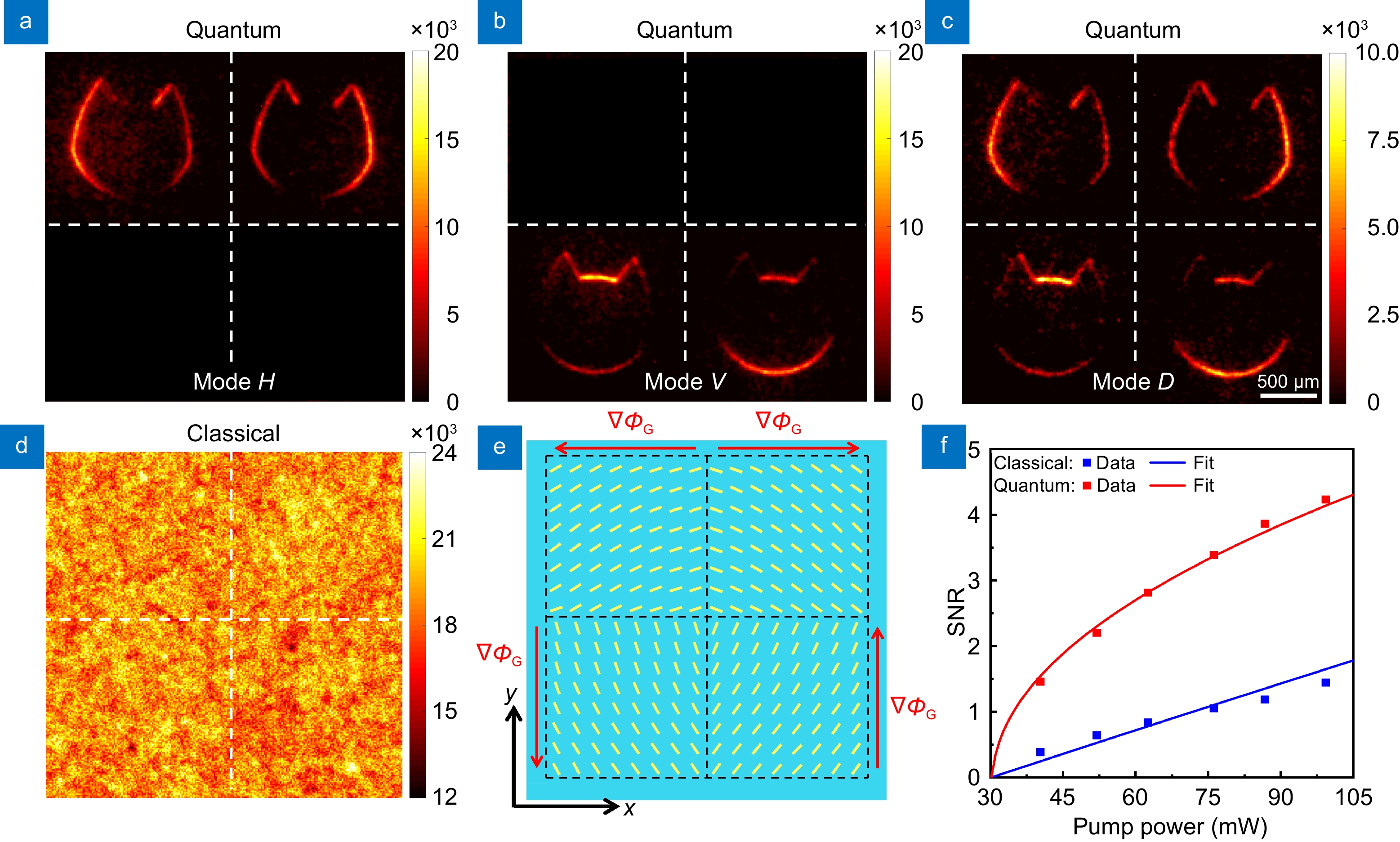 Figure 3. Experimental results of analog operation. (a–c) Experimental results of quantum analog operation in three modes, respectively. (d) Experimental results of classical analog operation in third mode. (e) Schematic of the detailed local optical axes of the four regions being designed on the metasurface. (f) The SNR in experimental imaging results of classical and quantum analog operation, respectively, under different pump powers.
Figure 3. Experimental results of analog operation. (a–c) Experimental results of quantum analog operation in three modes, respectively. (d) Experimental results of classical analog operation in third mode. (e) Schematic of the detailed local optical axes of the four regions being designed on the metasurface. (f) The SNR in experimental imaging results of classical and quantum analog operation, respectively, under different pump powers.Differential operators {\hat{F}}_{1}, \mathrm{ }{\hat{F}}_{2} , {\hat{F}}_{3} , and {\hat F_4} can be constituted by the optical elements of the imaging path, which correspond to the four imaging results on the ICCD. Due to the polarization entanglement, the imaging results can be controlled remotely by the polarization angle of the trigger photon, which can be considered as a mode selector. In our experimental demonstration, the four differential operations, which are required by quantitative phase reconstruction, can be generated simultaneously [Fig. 3(a–c)]. Besides, the proposed metasurface-integrated quantum analog operation system can improve the spatial resolution55 by enhancing the image edges (see Section 7 in the Supplementary information).
Quantum analog operation improves the signal-to-noise ratio
In order to demonstrate the preponderances of the metasurface-integrated quantum analog operation system, two different system configurations, namely continuous acquisition and trigger detection, are used to represent the imaging methods of classical and quantum analog operations, respectively. All experimental imaging results are captured by the intensified charge coupled device (ICCD) at a low signal photon level. In the imaging method based on classical analog operation, the operation mode of the ICCD is set to internal trigger, which causes the ambient noise to be captured together with the signal photons. When the ambient shot noise is equivalent to the signal level (even higher than), the system with a low SNR will result in signal invisibility [Fig. 3(d)]. Here, the SNR of classical imaging method can be expressed as48
SNR_{\mathrm{C}}=\frac{N_{\mathrm{s}}}{\sqrt{N_{\mathrm{s}}+N_{\mathrm{n}}}}\mathrm{~,} (10) where {N_{\mathrm{s}}} and {N_{\mathrm{n}}} denote the counts of signal and noise photons per second, respectively. In the metasurface-integrated quantum analog operation system, the trigger photon can be used as the external trigger signal of the ICCD to improve the SNR. The operating mode of the ICCD is set to the external trigger, and the shutter will only open when the external trigger signal is received. The shutter width is set to 4 ns, eliminating most of the ambient noise. Therefore, the SNR of the quantum imaging method can be written as48
SNR_{\mathrm{Q}}=\frac{hN_{\mathrm{s}}}{\sqrt{hN_{\mathrm{s}}+\epsilon N_{\mathrm{n}}}}\mathrm{~,} (11) where h is the coincidence-to-single counts ratio of entanglement source and \epsilon is the proportion coefficient of ambient noise photons falling within the gate width time. In the case of \epsilon \ll h , the SNR of the imaging system can be significantly improved. As shown in Fig. 3(f), when the pump power is 90{\mathrm{ mW}} , quantum imaging increases the SNR to 2.69 times compared to the classical imaging. Therefore, by using the metasurface-integrated quantum analog operation system with a non-local trigger detection, the SNR of differential results are clearly enhanced under the same low signal conditions.
Phase reconstruction via metasurface-integrated quantum analog operation
In order to illustrate the operating principle of the metasurface-integrated quantum analog operation system in quantitative phase imaging, some patterns shaped are etched on a glass substrate (see Section 8 in the Supplementary information). In the experiment, the trigger photon is first set to \left| D \right\rangle . Then, the four bias imaging results on the ICCD are combined to obtain the phase gradient in x- and y-directions [Fig. 4(a, b)]. Subsequently, \partial \varphi (x,y)/\partial x and \partial \varphi (x,y)/\partial y are superimposed to obtain the two-dimensional (2D) phase gradient \nabla \varphi (x,y) [Fig. 4(c)]. According to Eq. (6), the normalized phase distribution can be acquired [Fig. 4(i)]. Furthermore, by performing the derivative operation on normalized phase distribution, the reconstructed 1D phase gradient \partial \phi (x,y)/\partial x and \partial \phi (x,y)/\partial y, and the 2D phase gradient \nabla \phi (x,y), can also be calculated [Fig. 4(d–f)].
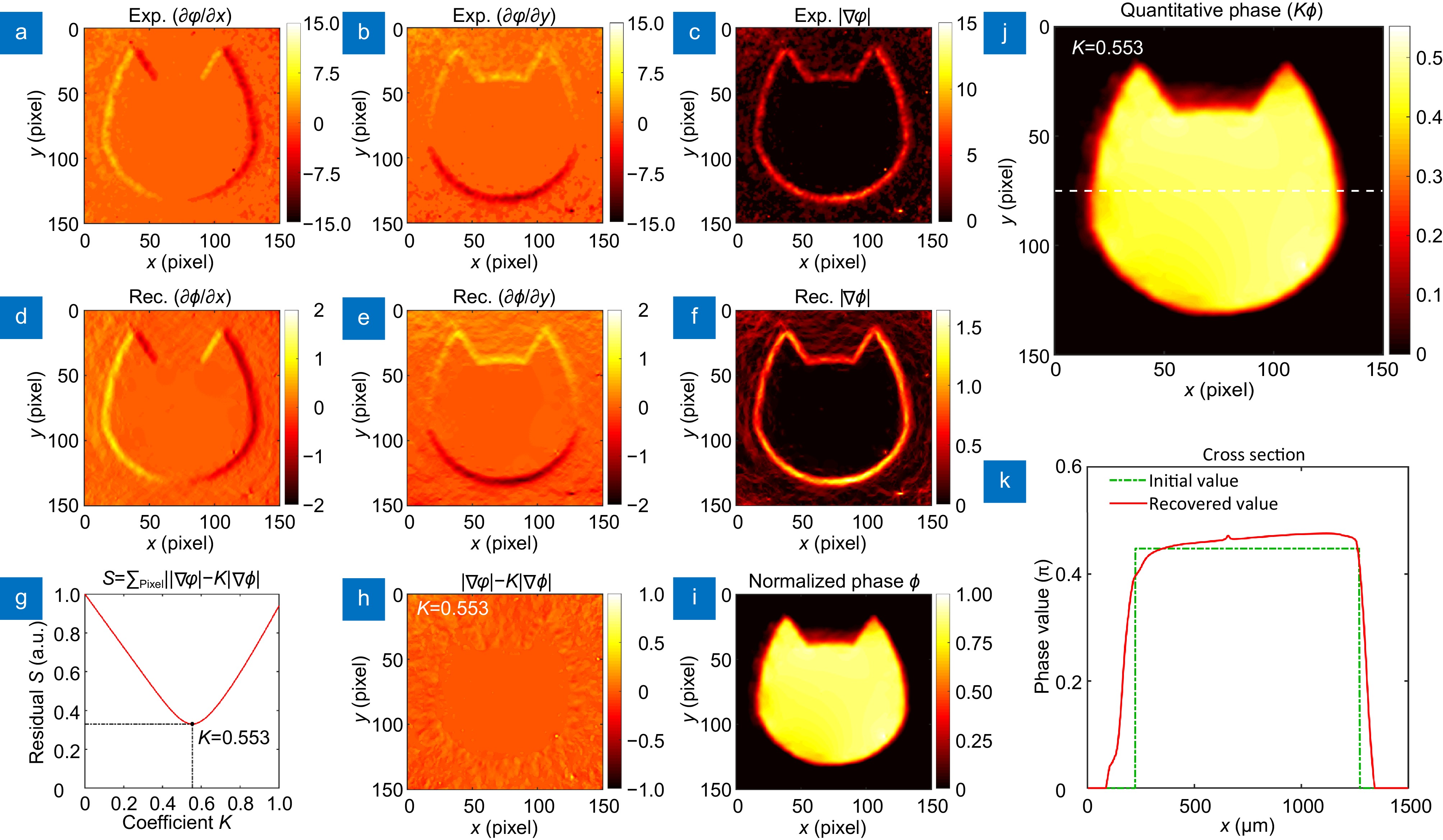 Figure 4. Process of quantitative phase reconstruction by Fourier integration. (a, b) Experimental measurement results of phase gradient in the x- and y-directions, respectively. (c) Experimental measurement results of 2D phase gradient. (d, e) Results of phase gradient reconstruction in the x- and y-directions, respectively, which is obtained by taking the derivative of the reconstructed normalized phase distribution. in the x- and y-directions, respectively. (f) Results of 2D phase gradient reconstruction. (g) Variation curve of the residual with coefficient K, which shows the process of solving the optimization problem. (h) Schematic diagram of minimum residuals. (i) Normalized results of phase reconstruction. (j) Quantitative results of phase reconstruction. (k) Results of the reconstructed depth corresponding to the white dotted lines.
Figure 4. Process of quantitative phase reconstruction by Fourier integration. (a, b) Experimental measurement results of phase gradient in the x- and y-directions, respectively. (c) Experimental measurement results of 2D phase gradient. (d, e) Results of phase gradient reconstruction in the x- and y-directions, respectively, which is obtained by taking the derivative of the reconstructed normalized phase distribution. in the x- and y-directions, respectively. (f) Results of 2D phase gradient reconstruction. (g) Variation curve of the residual with coefficient K, which shows the process of solving the optimization problem. (h) Schematic diagram of minimum residuals. (i) Normalized results of phase reconstruction. (j) Quantitative results of phase reconstruction. (k) Results of the reconstructed depth corresponding to the white dotted lines.As shown in Fig. 4(g), the optimization problem \min {\mathrm{ }}S(K) is solved to acquire the optimal normalization coefficient K = 0.445 . Here, Fig. 4(h) represents the pattern of |\nabla \varphi (x,y) - K\nabla \phi (x,y)| when K = 0.445 . Eventually, the results of quantitative phase reconstruction are shown in Fig. 4(j). To demonstrate the accuracy of our proposed metasurface-integrated quantum analog operation system for realizing quantitative phase reconstruction, the relative errors \vartheta of the white dashed lines in Fig. 4(j) is calculated. As shown the results of reconstructed depth value in Fig. 4(k), the relative error of the cat is 2.71\% (see Section 9 in the Supplementary information). To illustrate the universality of our scheme, quantitative phase reconstruction of more types of phase objects is demonstrated. Patterns in the shape of "01" and "Tai Chi" are also etched onto the glass substrate. The experimental phase gradients of the two patterns are shown in Fig. 5(a), 5(b), 5(e), and 5(f). Through quantitative reconstruction algorithm, the quantitative phase distribution of the two patterns can be obtained, respectively [Fig. 5(c) and 5(g)]. Meanwhile, Fig. 5(d) and 5(h) are the reconstructed phase value corresponding to the white dotted lines of "01" and "Tai Chi", respectively.
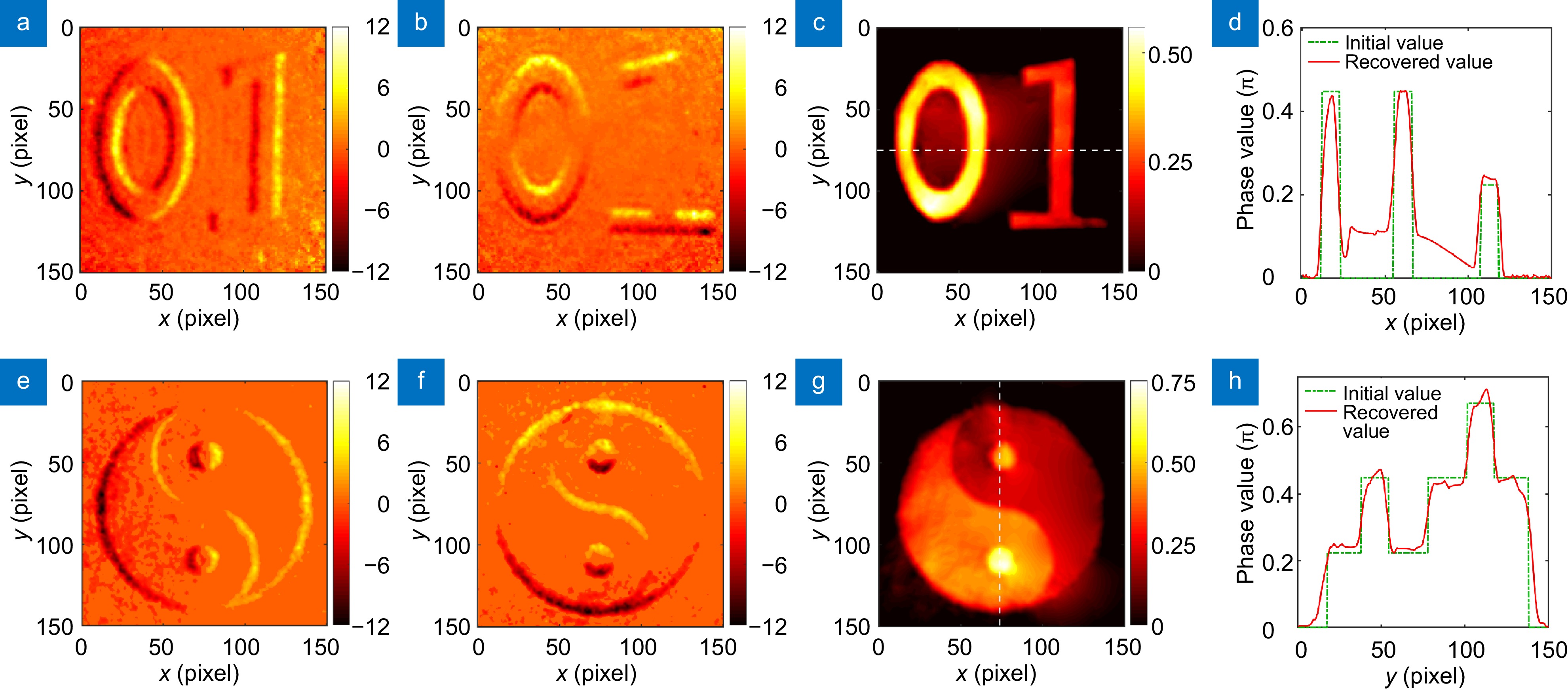 Figure 5. Quantitative phase reconstruction results. (a, b, e, f) The measured phase gradient results of phase objects- "01" and "Tai Chi", respectively. (c, g) Quantitative phase reconstruction results of "01" and "Tai Chi", respectively. (d, h) Results of the reconstructed phase value corresponding to the white dotted lines of "01" and "Tai Chi", respectively.
Figure 5. Quantitative phase reconstruction results. (a, b, e, f) The measured phase gradient results of phase objects- "01" and "Tai Chi", respectively. (c, g) Quantitative phase reconstruction results of "01" and "Tai Chi", respectively. (d, h) Results of the reconstructed phase value corresponding to the white dotted lines of "01" and "Tai Chi", respectively.Conclusions
In the proposed metasurface-integrated quantum analog operation system, the non-local correlation of polarized entangled photon pairs is a prerequisite for the remote switching of mode selection. Through the polarization selection of the trigger photon, the imaging photon can be induced to collapse to the desired state simultaneously, realizing the analog operation in different modes. As a demonstration, four differential operations in the metasurface-integrated quantum analog operation system are designed for realizing quantitative phase reconstruction. Theoretically, more diverse operational modes are expected to be achieved by designing multiple functional structures on the metasurface, which can be freely switched by trigger photons. Therefore, the proposed metasurface-integrated quantum analog operation system is extremely malleable. Furthermore, the quantum analog operation provides clearer imaging results than classical analog operations. When the signal is equivalent (even smaller than) to the ambient noise, the signal in the classical method will be drowned by ambient noise inevitably. However, in the quantum method, the sister photon of the signal photon can be used as an external trigger signal to control the switch of the detector, which suppresses the ambient noise effectively.
In conclusion, based on multi-channel metasurface and quantum entanglement source, a simple and integrated quantum analog operation system is proposed to realize quantitative phase reconstruction with a high SNR under a low signal photon level. Specifically, due to the non-local correlation of entangled photons, the mode selection of the metasurface-integrated quantum analog operation system can be switched remotely without changing the imaging arm. Notably, the four differential operators required for phase reconstruction can be obtained simultaneously by an integrated metasurface. As a result, the relative error of quantitative phase reconstruction is 2.71 %, which indicate the accuracy of the proposed method. Besides, the SNR of differential results is improved by 2.69 times compared with the classical approach. The results demonstrate our proposed scheme may potentially empower the metasurface in optical chip, wave function reconstruction, and label-free biology imaging.
Acknowledgements
We thank the Professor Lingjun Kong at Beijing Institute of Technology for his helpful discussions. This work was supported by the National Natural Science Foundation of China (Grants No. 62221002, Grants No. 12174097).
Author contributions
All authors commented on the manuscript. Such as: Q. L. performed experiment measurements, prepared the figures, and wrote the first draft of the manuscript. M. L. performed the design optimization and performed experiment measurements. S. L., J. L., and S. C. performed manuscript and figure optimizations, provided metasurface designs, and prepared microscopic samples. S. W. supervised the project. H. L. conceived the original idea, supervised the project. All authors contributed to finalizing the manuscript.
Competing interests
The authors declare no competing financial interests.
-
References
[1] Lemos GB, Borish V, Cole GD et al. Quantum imaging with undetected photons. Nature 512, 409–412 (2014). doi: 10.1038/nature13586 [2] Park Y, Depeursinge C, Popescu G. Quantitative phase imaging in biomedicine. Nat Photonics 12, 578–589 (2018). doi: 10.1038/s41566-018-0253-x [3] Kwon H, Arbabi E, Kamali SM et al. Single-shot quantitative phase gradient microscopy using a system of multifunctional metasurfaces. Nat Photonics 14, 109–114 (2020). doi: 10.1038/s41566-019-0536-x [4] Wang B, Rong KX, Maguid E et al. Probing nanoscale fluctuation of ferromagnetic meta-atoms with a stochastic photonic spin Hall effect. Nat Nanotechnol 15, 450–456 (2020). doi: 10.1038/s41565-020-0670-0 [5] Chen ZP, Zhang B, Pan YM et al. Quantum wave function reconstruction by free-electron spectral shearing interferometry. Sci Adv 9, eadg8516 (2023). doi: 10.1126/sciadv.adg8516 [6] Wang XW, Hao HJ, He XY et al. Advances in information processing and biological imaging using flat optics. Nat Rev Electr Eng 1, 391–411 (2024). doi: 10.1038/s44287-024-00057-2 [7] Shaked NT, Boppart SA, Wang LV et al. Label-free biomedical optical imaging. Nat Photonics 17, 1031–1041 (2023). doi: 10.1038/s41566-023-01299-6 [8] Hu CF, Field JJ, Kelkar V et al. Harmonic optical tomography of nonlinear structures. Nat Photonics 14, 564–569 (2020). doi: 10.1038/s41566-020-0638-5 [9] Liu YF, Yu PP, Wu YJ et al. Optical single-pixel volumetric imaging by three-dimensional light-field illumination. Proc Natl Acad Sci USA 120, e2304755120 (2023). doi: 10.1073/pnas.2304755120 [10] Bauer T, Orlov S, Peschel U et al. Nanointerferometric amplitude and phase reconstruction of tightly focused vector beams. Nat Photonics 8, 23–27 (2014). doi: 10.1038/nphoton.2013.289 [11] Bai BJ, Yang XL, Li YZ et al. Deep learning-enabled virtual histological staining of biological samples. Light Sci Appl 12, 57 (2023). doi: 10.1038/s41377-023-01104-7 [12] Zernike F. How I discovered phase contrast. Science 121, 345–349 (1955). doi: 10.1126/science.121.3141.345 [13] Allen RD, David GB, Nomarski G. The Zeiss-Nomarski differential interference equipment for transmitted-light microscopy. Z Wiss Mikrosk 69, 193–221 (1969). [14] Huang ZZ, Cao LC. Quantitative phase imaging based on holography: trends and new perspectives. Light Sci Appl 13, 145 (2024). doi: 10.1038/s41377-024-01453-x [15] Chaumet PC, Bon P, Maire G et al. Quantitative phase microscopies: accuracy comparison. Light Sci Appl 13, 288 (2024). doi: 10.1038/s41377-024-01619-7 [16] Stav T, Faerman A, Maguid E et al. Quantum entanglement of the spin and orbital angular momentum of photons using metamaterials. Science 361, 1101–1104 (2018). doi: 10.1126/science.aat9042 [17] Wang K, Titchener JG, Kruk SS et al. Quantum metasurface for multiphoton interference and state reconstruction. Science 361, 1104–1108 (2018). doi: 10.1126/science.aat8196 [18] Georgi P, Massaro M, Luo KH et al. Metasurface interferometry toward quantum sensors. Light Sci Appl 8, 70 (2019). doi: 10.1038/s41377-019-0182-6 [19] Solntsev AS, Agarwal GS, Kivshar YS. Metasurfaces for quantum photonics. Nat Photonics 15, 327–336 (2021). doi: 10.1038/s41566-021-00793-z [20] Li M, Hu GW, Chen X et al. Topologically reconfigurable magnetic polaritons. Sci Adv 8, eadd6660 (2022). doi: 10.1126/sciadv.add6660 [21] Wang XW, Wang H, Wang JL et al. Single-shot isotropic differential interference contrast microscopy. Nat Commun 14, 2063 (2023). doi: 10.1038/s41467-023-37606-6 [22] Ma QC, Li GX. Miniature meta-device for dynamic control of Airy beam. Opto-Electron Adv 7, 240166 (2024). doi: 10.29026/oea.2024.240166 [23] Luo XG. Principles of electromagnetic waves in metasurfaces. Sci China Phys Mech Astron 58, 594201 (2015). doi: 10.1007/s11433-015-5688-1 [24] Zhang JH, ElKabbash M, Wei R et al. Plasmonic metasurfaces with 42.3% transmission efficiency in the visible. Light Sci Appl 8, 53 (2019). doi: 10.1038/s41377-019-0164-8 [25] Fan QB, Liu MZ, Zhang C et al. Independent amplitude control of arbitrary orthogonal states of polarization via dielectric metasurfaces. Phys Rev Lett 125, 267402 (2020). doi: 10.1103/PhysRevLett.125.267402 [26] Xie X, Pu MB, Jin JJ et al. Generalized pancharatnam-berry phase in rotationally symmetric meta-atoms. Phys Rev Lett 126, 183902 (2021). doi: 10.1103/PhysRevLett.126.183902 [27] Kort-Kamp WJM, Azad AK, Dalvit DAR. Space-time quantum metasurfaces. Phys Rev Lett 127, 043603 (2021). doi: 10.1103/PhysRevLett.127.043603 [28] Guo YH, Zhang SC, Pu MB et al. Spin-decoupled metasurface for simultaneous detection of spin and orbital angular momenta via momentum transformation. Light Sci Appl 10, 63 (2021). doi: 10.1038/s41377-021-00497-7 [29] Xu DY, Xu WH, Yang Q et al. All-optical object identification and three-dimensional reconstruction based on optical computing metasurface. Opto-Electron Adv 6, 230120 (2023). doi: 10.29026/oea.2023.230120 [30] Silva A, Monticone F, Castaldi G et al. Performing mathematical operations with metamaterials. Science 343, 160–163 (2014). doi: 10.1126/science.1242818 [31] Solli D, Jalali B. Analog optical computing. Nat Photonics 9, 704–706 (2015). doi: 10.1038/nphoton.2015.208 [32] Zhou Y, Zheng HY, Kravchenko II et al. Flat optics for image differentiation. Nat Photonics 14, 316–323 (2020). doi: 10.1038/s41566-020-0591-3 [33] Gao YJ, Wang Z, Jiang Y et al. Multichannel distribution and transformation of entangled photons with dielectric metasurfaces. Phys Rev Lett 129, 023601 (2022). doi: 10.1103/PhysRevLett.129.023601 [34] Liu SQ, Chen SZ, Wen SC et al. Photonic spin Hall effect: fundamentals and emergent applications. Opto-Electron Sci 1, 220007 (2022). doi: 10.29026/oes.2022.220007 [35] Zhang XD, Liu YL, Han JC et al. Chiral emission from resonant metasurfaces. Science 377, 1215–1218 (2022). doi: 10.1126/science.abq7870 [36] Li L, Wang S, Zhao F et al. Single-shot deterministic complex amplitude imaging with a single-layer metalens. Sci Adv 10, eadl0501 (2024). doi: 10.1126/sciadv.adl0501 [37] Yao J, Hsu WL, Liang Y et al. Nonlocal metasurface for dark-field edge emission. Sci Adv 10, eadn2752 (2024). doi: 10.1126/sciadv.adn2752 [38] Ni XJ, Kildishev AV, Shalaev VM. Metasurface holograms for visible light. Nat Commun 4, 2807 (2013). doi: 10.1038/ncomms3807 [39] Zheng GX, Mühlenbernd H, Kenney M et al. Metasurface holograms reaching 80% efficiency. Nat Nanotechnol 10, 308–312 (2015). doi: 10.1038/nnano.2015.2 [40] Colburn S, Zhan AL, Majumdar A. Metasurface optics for full-color computational imaging. Sci Adv 4, eaar2114 (2018). doi: 10.1126/sciadv.aar2114 [41] Liu Y, Huang MC, Chen QK et al. Single planar photonic chip with tailored angular transmission for multiple-order analog spatial differentiator. Nat Commun 13, 7944 (2022). doi: 10.1038/s41467-022-35588-5 [42] Cotrufo M, Sulejman SB, Wesemann L et al. Reconfigurable image processing metasurfaces with phase-change materials. Nat Commun 15, 4483 (2024). doi: 10.1038/s41467-024-48783-3 [43] Ji AQ, Song JH, Li QT et al. Quantitative phase contrast imaging with a nonlocal angle-selective metasurface. Nat Commun 13, 7848 (2022). doi: 10.1038/s41467-022-34197-6 [44] Wu QY, Zhou JX, Chen XY et al. Single-shot quantitative amplitude and phase imaging based on a pair of all-dielectric metasurfaces. Optica 10, 619–625 (2023). doi: 10.1364/OPTICA.483366 [45] Liu JW, Yang Q, Shou YC et al. Metasurface-assisted quantum nonlocal weak-measurement microscopy. Phys Rev Lett 132, 043601 (2024). doi: 10.1103/PhysRevLett.132.043601 [46] Brida G, Genovese M, Berchera IR. Experimental realization of sub-shot-noise quantum imaging. Nat Photonics 4, 227–230 (2010). doi: 10.1038/nphoton.2010.29 [47] Morris PA, Aspden RS, Bell JEC et al. Imaging with a small number of photons. Nat Commun 6, 5913 (2015). doi: 10.1038/ncomms6913 [48] Johnson S, McMillan A, Torre C et al. Single-pixel imaging with heralded single photons. Opt Continuum 1, 826–833 (2022). doi: 10.1364/OPTCON.458248 [49] Ling XH, Zhou XX, Yi XN et al. Giant photonic spin Hall effect in momentum space in a structured metamaterial with spatially varying birefringence. Light Sci Appl 4, e290 (2015). doi: 10.1038/lsa.2015.63 [50] Zhou JX, Qian HL, Zhao JX et al. Two-dimensional optical spatial differentiation and high-contrast imaging. Natl Sci Rev 8, nwaa176 (2021). doi: 10.1093/nsr/nwaa176 [51] Kwiat PG, Waks E, White AG et al. Ultrabright source of polarization-entangled photons. Phys Rev A 60, R773–R776 (1999). doi: 10.1103/PhysRevA.60.R773 [52] Kong LJ, Sun YF, Zhang FR et al. High-dimensional entanglement-enabled holography. Phys Rev Lett 130, 053602 (2023). doi: 10.1103/PhysRevLett.130.053602 [53] Clauser JF, Shimony A. Bell’s theorem. Experimental tests and implications. Rep Prog Phys 41, 1881–1927 (1978). doi: 10.1088/0034-4885/41/12/002 [54] Horodecki R, Horodecki P, Horodecki M et al. Quantum entanglement. Rev Mod Phys 81, 865–942 (2009). doi: 10.1103/RevModPhys.81.865 [55] He Z, Zhang YD, Tong X et al. Quantum microscopy of cells at the Heisenberg limit. Nat Commun 14, 2441 (2023). doi: 10.1038/s41467-023-38191-4 -
Supplementary Information
Supplementary information for Phase reconstruction via metasurface-integrated quantum analog operation 
-
Access History
-
Figure 1.
Phase reconstruction via metasurface-integrated quantum analog operation. (a) Schematic of non-local mode selection by metasurface-integrated quantum analog operation.
{\hat{F}}_{1} {\hat{F}}_{2} {\hat{F}}_{3} {\hat F_4} -
Figure 2.
Experimental setup. Setup schematic: HWP, half-wave plate; QWP, quarter-wave plate; PBS, polarization beam splitter; M, mirror; QC, quartz crystal; L, Lens; BBOs, β-BaB2O4 crystals; LPF, long-pass filter; FC, fiber coupler; BS, beam splitter; SMF, single mode fiber; SPCM, single photon counting module; ICCD, intensified charge coupled device. Inset, the experimental results of the polarization interference curves.
-
Figure 3.
Experimental results of analog operation. (a–c) Experimental results of quantum analog operation in three modes, respectively. (d) Experimental results of classical analog operation in third mode. (e) Schematic of the detailed local optical axes of the four regions being designed on the metasurface. (f) The SNR in experimental imaging results of classical and quantum analog operation, respectively, under different pump powers.
-
Figure 4.
Process of quantitative phase reconstruction by Fourier integration. (a, b) Experimental measurement results of phase gradient in the x- and y-directions, respectively. (c) Experimental measurement results of 2D phase gradient. (d, e) Results of phase gradient reconstruction in the x- and y-directions, respectively, which is obtained by taking the derivative of the reconstructed normalized phase distribution. in the x- and y-directions, respectively. (f) Results of 2D phase gradient reconstruction. (g) Variation curve of the residual with coefficient K, which shows the process of solving the optimization problem. (h) Schematic diagram of minimum residuals. (i) Normalized results of phase reconstruction. (j) Quantitative results of phase reconstruction. (k) Results of the reconstructed depth corresponding to the white dotted lines.
-
Figure 5.
Quantitative phase reconstruction results. (a, b, e, f) The measured phase gradient results of phase objects- "01" and "Tai Chi", respectively. (c, g) Quantitative phase reconstruction results of "01" and "Tai Chi", respectively. (d, h) Results of the reconstructed phase value corresponding to the white dotted lines of "01" and "Tai Chi", respectively.


 E-mail Alert
E-mail Alert RSS
RSS

 DownLoad:
DownLoad: